Advertisements
Advertisements
प्रश्न
Find the sum of the lengths of the bases of a trapezium whose area is 4.2 m2 and whose height is 280 cm.
उत्तर
Area of the trapezium = 4.2 m2
Height = 280 cm \[=\frac{280}{100}m = 2.8 m\]
Area of trapezium\[= \frac{1}{2} \times(\text{ Sum of the parallel bases })\times(\text{ Height })\]
\[4.2 =\frac{1}{2}\times(\text{ Sum of the parallel bases })\times2.8\]
\[4 . 2 \times 2 = (\text{ Sum of the parallel bases })\times2.8\]
\[\text{ Sum of the parallel bases }= \frac{8 . 4}{2 . 8} = 3 m\]
APPEARS IN
संबंधित प्रश्न
The area of a trapezium is 34 cm2 and the length of one of the parallel sides is 10 cm and its height is 4 cm. Find the length of the other parallel side.
Find the area, in square metres, of the trapezium whose bases and altitude is as under:
bases = 8 m and 60 dm, altitude = 40 dm
Find the area of a trapezium whose parallel sides of lengths 10 cm and 15 cm are at a distance of 6 cm from each other. Calculate this area as
the sum of the areas of two triangles and one rectangle.
The area of a trapezium is 960 cm2. If the parallel sides are 34 cm and 46 cm, find the distance between them.
The area of a trapezium is 91 cm2 and its height is 7 cm. If one of the parallel sides is longer than the other by 8 cm, find the two parallel sides.
The area of a trapezium is 279 sq.cm and the distance between its two parallel sides is 18 cm. If one of its parallel sides is longer than the other side by 5 cm, find the lengths of its parallel sides.
The area of a trapezium is 180 sq.cm and its height is 9 cm. If one of the parallel sides is longer than the other by 6 cm. Find the length of the parallel sides.
A window is in the form of trapezium whose parallel sides are 105 cm and 50 cm respectively and the distance between the parallel sides is 60 cm. Find the cost of the glass used to cover the window at the rate of ₹ 15 per 100 sq.cm
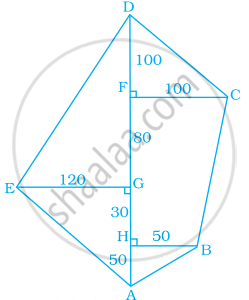
Find the area of the following fields. All dimensions are in metres.
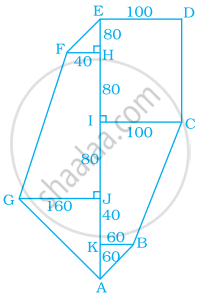
Find the area of the following fields. All dimensions are in metres.