Advertisements
Advertisements
प्रश्न
Find, by integration, the volume of the solid generated by revolving about the x axis, the region enclosed by y = e-2x, y = 0, x = 0 and x = 1
उत्तर
Since revolution is made about the x-axis, the volume of the solid generated is given
V = `pi int_"a"^"b" y^2 "d"x`
= `pi int_0^1 ("e"^(-2x))^2 "d"x`
= `pi int_0^1 "e"^(- 4x) "d"x`
= `pi["e"^(- 4x)/(- 4)]_0^1`
= `pi["e"^(- 4)/(- 4) + 1/4]`
= `pi/4 [1 - "e"^-4]`
Required volume = `pi/4 [1 - "e"^-4]` cubic units
APPEARS IN
संबंधित प्रश्न
Find by integration, the volume of the solid generated by revolving about the x-axis, the region enclosed by y = 2x2, y = 0 and x = 1
Find, by integration, the volume of the solid generated by revolving about the y axis, the region enclosed by x2 = 1 + y and y = 3
The region enclosed between the graphs of y = x and y = x2 is denoted by R. Find the volume generated when R is rotated through 360° about x-axis
Find, by integration, the volume of the container which is in the shape of a right circular conical frustum as shown in the Fig 9.46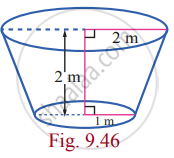
A watermelon has an ellipsoid shape which can be obtained by revolving an ellipse with major-axis 20 cm and minor-axis 10 cm about its major-axis. Find its volume using integration
Choose the correct alternative:
The volume of solid of revolution of the region bounded by y2 = x(a – x) about the x-axis is
