Question

Find the equation of the ellipse whose focus is (1, −2), the directrix 3x − 2y + 5 = 0 and eccentricity equal to 1/2.

 

Answer 1

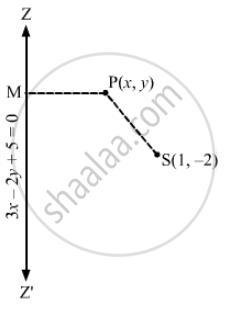
\[\text{ Let S(1, - 2) be the focus and ZZ' be the directrix } . \]
\[\text{ Let P(x, y) be any point on the ellipse and let PM be the perpendicular from P on the directix } . \]
\[\text{ Then by the definition of an ellipse, we have:}  \]
\[SP = e .\text{  PM, where e } = \frac{1}{2}\]
\[ \Rightarrow S P^2 = e^2 . P M^2 \]
\[ \Rightarrow (x - 1 )^2 + (y + 2 )^2 = \left( \frac{1}{2} \right)^2 . \left| \frac{3x - 2y + 5}{\sqrt{(3 )^2 + ( - 2 )^2}} \right|^2 \]
\[ \Rightarrow x^2 + 1 - 2x + y^2 + 4 + 4y = \left( \frac{1}{4} \right) . \left| \frac{9 x^2 + 4 y^2 + 25 - 12xy - 20y + 30x}{13} \right|\]
\[ \Rightarrow 52( x^2 + 1 - 2x + y^2 + 4 + 4y) = 9 x^2 + 4 y^2 + 25 - 12xy - 20y + 30x\]
\[ \Rightarrow 52 x^2 + 52 - 104x + 52 y^2 + 208 + 208y = 9 x^2 + 4 y^2 + 25 - 12xy - 20y + 30x\]
\[ \Rightarrow 43 x^2 + 48 y^2 - 134x + 228y + 12xy + 235 = 0\]
\[\text{ This is the equation of the required ellipse }  .\]