Question

Find graphically the vertices of the triangle, whose sides are given by 3y = x + 18, x + 7y = 22 and y + 3x = 26.

Answer 1

The given equation are :
3y = x + 18 ...(1)
x + 7y = 22 ...(2)
y + 3x = 26 ...(3)
3y = x + 18
⇒ x = 3y - 18
Corresponding values of x and y can be tabulated as :

x	0	-3	-6
y	6	5	4

Plotting points (0, 6), (-3, 5) and (-6, 4) joining them, we get a line l₁ which is the graph of equation (1).

Again, x + 7y = 22
⇒ x = 22 - 7y
Corresponding values of x and y can be tabulated as :

x	1	8	-6
y	3	2	4

Plotting points (1, 3), (8, 2), (-6, 4) and joining them, we get a line l₂ which is the graph of equation (2).

Also, y + 3x = 26
⇒  y = 26 - 3x
Corresponding values of x and y can be tabulated as :

x	7	8	9
y	5	2	-1

Plotting points (7, 5), (8, 2), (9, -1) and joining them, we get a line l₃ which is the graph of equation (3).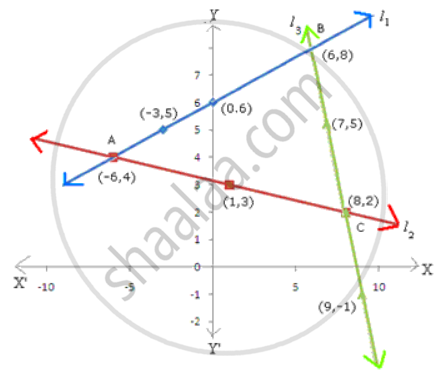

It can be seen that the lines l₁, l₂ and l₃ intersect each other to form triangle ABC.
The verticles of ΔABC are A(-6, 4), B(6, 8) and C(8, 2).