Advertisements
Advertisements
प्रश्न
Find graphically the vertices of the triangle, whose sides are given by 3y = x + 18, x + 7y = 22 and y + 3x = 26.
उत्तर
The given equation are :
3y = x + 18 ...(1)
x + 7y = 22 ...(2)
y + 3x = 26 ...(3)
3y = x + 18
⇒ x = 3y - 18
Corresponding values of x and y can be tabulated as :
| x | 0 | -3 | -6 |
| y | 6 | 5 | 4 |
Plotting points (0, 6), (-3, 5) and (-6, 4) joining them, we get a line l1 which is the graph of equation (1).
Again, x + 7y = 22
⇒ x = 22 - 7y
Corresponding values of x and y can be tabulated as :
| x | 1 | 8 | -6 |
| y | 3 | 2 | 4 |
Plotting points (1, 3), (8, 2), (-6, 4) and joining them, we get a line l2 which is the graph of equation (2).
Also, y + 3x = 26
⇒ y = 26 - 3x
Corresponding values of x and y can be tabulated as :
| x | 7 | 8 | 9 |
| y | 5 | 2 | -1 |
Plotting points (7, 5), (8, 2), (9, -1) and joining them, we get a line l3 which is the graph of equation (3).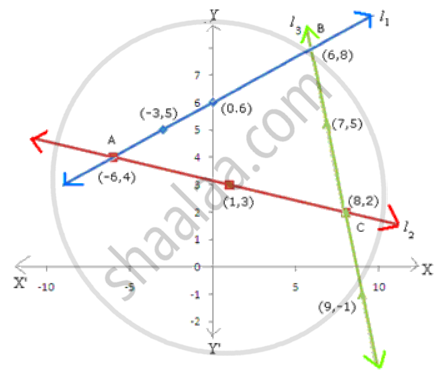
It can be seen that the lines l1, l2 and l3 intersect each other to form triangle ABC.
The verticles of ΔABC are A(-6, 4), B(6, 8) and C(8, 2).
APPEARS IN
संबंधित प्रश्न
Solve graphically the simultaneous equations given below. Take the scale as 2 cm = 1 unit on both the axes.
x - 2y - 4 = 0
2x + y = 3
Solve the following equations graphically :
x + 3y = 8
3x = 2 + 2y
Solve the following equations graphically :
2x + 4y = 7
3x + 8y = 10
Solve the following equations graphically :
`2 + (3y)/x = (6)/x`
`(6x)/y - 5 = (4)/y`
Solve the following equations graphically :
x+ 2y - 7 = 0
2x - y - 4 = 0
Find graphically the vertices of the triangle, whose sides have the equations 2y - x = 8, 5y -x = 14 and y = 2x - 1.
Solve the following system of equations graphically
x - y + 1 = 0
4x + 3y = 24
Draw the graph of the following equations :
3x + 2y + 6 = 0
3x + 8y - 12 = 0
Also, determine the co-ordinates of the vertices of the triangle formed by these lines and x-axis.
Solve the following system of equations graphically:
6x - 3y + 2 = 7x + 1
5x + 1 = 4x - y + 2
Also, find the area of the triangle formed by these lines and x-axis in each graph.
Solve graphically
y = 2x + 1, y + 3x – 6 = 0
