Advertisements
Advertisements
प्रश्न
Find the lengths of the medians of a triangle whose vertices are A(–1, 1), B(5, –3) and C(3, 5).
उत्तर
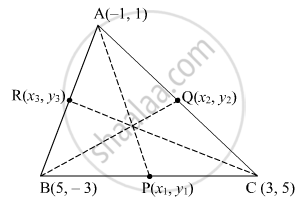
Let the medians meet the lines BC, AC and AB at points be
\[P\left( x_1 , y_1 \right)\]
\[Q\left( x_2 , y_2 \right)\] and
\[R\left( x_3 , y_3 \right)\]respectively.
P is thus the mid point of line BC
\[P\left( x_1 , y_1 \right) = \left( \frac{5 + 3}{2}, \frac{5 - 3}{2} \right) = \left( 4, 1 \right)\]
\[AP = \sqrt{\left( -4 - 1 \right)^2 + \left( 1 - 1 \right)^2} = \sqrt{25} = 5\]
Q is the mid point of line AC.
\[Q\left( x_2 , y_2 \right) = \left( \frac{- 1 + 3}{2}, \frac{1 + 5}{2} \right) = \left( 1, 3 \right)\]
\[BQ = \sqrt{\left( 5 - 1 \right)^2 + \left( - 3 - 3 \right)^2} = \sqrt{16 + 36} = \sqrt{52} = 2\sqrt{13}\]
R is the mid point of AB.
\[R\left( x_3 , y_3 \right) = \left( \frac{- 1 + 5}{2}, \frac{1 - 3}{2} \right) = \left( 2, - 1 \right)\]
\[RC = \sqrt{\left( 3 - 2 \right)^2 + \left( -1 - 5 \right)^2} = \sqrt{1 + 36} = \sqrt{37}\]
संबंधित प्रश्न
Find the centroid of the triangle whose vertice is given below.
(–7, 6), (2, –2), (8, 5)
Find the centroid of the triangle whose vertice is given below.
(3, –5), (4, 3), (11, –4)
Find the centroid of the triangle whose vertice is given below.
(4, 7), (8, 4), (7, 11)
In ∆ABC, G (–4, –7) is the centroid. If A (–14, –19) and B(3, 5) then find the co–ordinates of C.
A(h, –6), B(2, 3) and C(–6, k) are the co–ordinates of vertices of a triangle whose centroid is G (1, 5). Find h and k.
In the following example, can the segment joining the given point form a triangle? If a triangle is formed, state the type of the triangle considering the side of the triangle.
L(6, 4), M(–5, –3), N(–6, 8)
In the following example, can the segment joining the given point form a triangle? If triangle is formed, state the type of the triangle considering side of the triangle.
P(–2, –6) , Q(–4, –2), R(–5, 0)
In the following example, can the segment joining the given points form a triangle? If triangle is formed, state the type of the triangle considering sides of the triangle.
A(√2, √2), B(−√2, −√2), C(−√6, √6)
Find the coordinates of centroid of the triangles if points D(–7, 6), E(8, 5) and F(2, –2) are the mid points of the sides of that triangle.

LMNP is a parallelogram. From the information given in the figure fill in the following boxes.
MN = cm
PN = cm
∠ M =
∠ N =
Find the coordinates of centroid of a triangle whose vertices are (4, 7), (8, 4) and (7, 11)
The coordinates of the vertices of a triangle ABC are A (–7, 6), B(2, –2) and C(8, 5). Find coordinates of its centroid.
Solution: Suppose A(x1, y1) and B(x2, y2) and C(x3, y3)
x1 = –7, y1 = 6 and x2 = 2, y2 = –2 and x3 = 8, y3 = 5
Using Centroid formula
∴ Coordinates of the centroid of a traingle
ABC = `((x_1 + x_2 + x_3)/3, (y_1 + y_2 + y_3)/3)`
= `(square/3, square/3)`
∴ Coordinates of the centroid of a triangle ABC = `(3/3, square)`
∴ Coordinates of the centroid of a triangle ABC = `(1 , square)`
Find the Y-coordinate of the centroid of a triangle whose vertices are (4, –3), (7, 5) and (–2, 1).
Find the centroid of the ΔABC whose vertices are A(–2, 0), B(7, –3) and C(6, 2).
