Advertisements
Advertisements
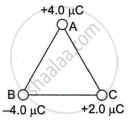
प्रश्न
Find out the amount of the work done to separate the charges at infinite distance.
उत्तर
The amount work done to separate the charges at infinity will be equal to potential energy.
Potential energy of the system U = `U_(q.2q) + U_(q-4q) + U_(2q-4q)`
`U = (kq(2q))/l + (kq(-4q))/l + (k2q(-4q))/l = (-10kq^2)/l`
Thus work done to seperate them to infinity W = U = `(-10kq^2)/l`
APPEARS IN
संबंधित प्रश्न
A cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the centre of the cube.
A point charge Q is placed at point 'O' as shown in the figure. Is the potential at point A, i.e. VA, greater, smaller or equal to potential, VB, at point B, when Q is (i) positive, and (ii) negative charge?
A point charge Q is placed at point O as shown in the figure. The potential difference VA – VB positive. Is the charge Q negative or positive?

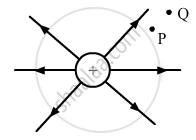
Figure shows the field lines due to a positive point charge. Give the sign of potential energy difference of a small negative charge between the points Q and P.
If a charge q0 is there in an electric field caused by several point charges qi. The potential energy of q0 is given by ________.
The work done in bringing a unit positive charge from infinite distance to a point at distance x from a positive charge Q is W. Then the potential at that point is ______.
Consider a uniform electric field in the z-direction. The potential is a constant ______.
- Assertion (A): An electron has a high potential energy when it is at a location associated with a more negative value of potential, and a low potential energy when at a location associated with a more positive potential.
- Reason (R): Electrons move from a region of higher potential to region of lower potential.
Select the most appropriate answer from the options given below:
In the circuit shown in figure initially, key K1 is closed and key K2 is open. Then K1 is opened and K2 is closed (order is important). [Take Q1′ and Q2′ as charges on C1 and C2 and V1 and V2 as voltage respectively.]

Then
- charge on C1 gets redistributed such that V1 = V2
- charge on C1 gets redistributed such that Q1′ = Q2′
- charge on C1 gets redistributed such that C1V1 + C2V2 = C1E
- charge on C1 gets redistributed such that Q1′ + Q2′ = Q
Justify your answers for each case.
State the significance of the negative value of electrostatic potential energy of a system of charges.
Three charges are placed at the corners of an equilateral triangle ABC of side 2.0 m as shown in the figure. Calculate the electric potential energy of the system of three charges.