Advertisements
Advertisements
प्रश्न
- Assertion (A): An electron has a high potential energy when it is at a location associated with a more negative value of potential, and a low potential energy when at a location associated with a more positive potential.
- Reason (R): Electrons move from a region of higher potential to region of lower potential.
Select the most appropriate answer from the options given below:
विकल्प
Both A and R are true and R is the correct explanation of A.
Both A and R are true but R is not the correct explanation of A.
A is true but R is false.
A is false and R is also false.
उत्तर
A is true but R is false.
Explanation:
When an electron is at a location associated with a negative value of potential, say -V, its potential energy is U = (-e)(-V) = eV. When an electron is at a location associated with a positive potential, say +V, its potential energy is U = (-e)(+V) = -eV. So, the assertion is true.
From higher to lower potential, current flows. Conventionally, electrons move from a lower to a greater potential when they flow in the opposite manner. So, the reason is false.
APPEARS IN
संबंधित प्रश्न
If one of the two electrons of a H2 molecule is removed, we get a hydrogen molecular ion `"H"_2^+`. In the ground state of an `"H"_2^+`, the two protons are separated by roughly 1.5 Å, and the electron is roughly 1 Å from each proton. Determine the potential energy of the system. Specify your choice of zero potential energy.
Find out the amount of the work done to separate the charges at infinite distance.
1 volt is equivalent to ______.
The work done in bringing a unit positive charge from infinite distance to a point at distance x from a positive charge Q is W. Then the potential at that point is ______.
In the circuit shown in figure initially, key K1 is closed and key K2 is open. Then K1 is opened and K2 is closed (order is important). [Take Q1′ and Q2′ as charges on C1 and C2 and V1 and V2 as voltage respectively.]

Then
- charge on C1 gets redistributed such that V1 = V2
- charge on C1 gets redistributed such that Q1′ = Q2′
- charge on C1 gets redistributed such that C1V1 + C2V2 = C1E
- charge on C1 gets redistributed such that Q1′ + Q2′ = Q
Calculate potential energy of a point charge – q placed along the axis due to a charge +Q uniformly distributed along a ring of radius R. Sketch P.E. as a function of axial distance z from the centre of the ring. Looking at graph, can you see what would happen if – q is displaced slightly from the centre of the ring (along the axis)?
- In a quark model of elementary particles, a neutron is made of one up quarks [charge (2/3) e] and two down quarks [charges –(1/3) e]. Assume that they have a triangle configuration with side length of the order of 10–15 m. Calculate electrostatic potential energy of neutron and compare it with its mass 939 MeV.
- Repeat above exercise for a proton which is made of two up and one down quark.
- Assertion (A): Work done in moving a charge around a closed path, in an electric field is always zero.
- Reason (R): Electrostatic force is a conservative force.
Justify your answers for each case.
State the significance of the negative value of electrostatic potential energy of a system of charges.
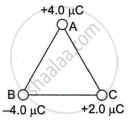
Three charges are placed at the corners of an equilateral triangle ABC of side 2.0 m as shown in the figure. Calculate the electric potential energy of the system of three charges.
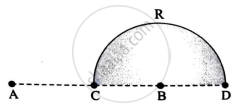
Charges (+q) and (–q) are placed at points A and B respectively which are a distance 2L apart. C is the midpoint between A and B. What is the work done in moving a charge +Q along the semicircle CRD?