Advertisements
Advertisements
प्रश्न
Find the roots of the following quadratic equations (if they exist) by the method of completing the square.
x2 - 4ax + 4a2 - b2 = 0
उत्तर
We have to find the roots of given quadratic equation by the method of completing the square. We have,
x2 - 4ax + 4a2 - b2 = 0
Now shift the constant to the right hand side,
x2 - 4ax = b2 - 4a2
Now add square of half of coefficient of x on both the sides,
x2 - 2(2a)x + (2a)2 = b2 - 4a2 + (2a)2
We can now write it in the form of perfect square as,
(x - 2a)2 = b2
Taking square root on both sides,
`(x-2a)=sqrt(b^2)`
So the required solution of x,
x = 2a ± b
x = 2a + b, 2a - b
APPEARS IN
संबंधित प्रश्न
Solve the following quadratic equation by completing square method : x2 + 10x + 21 = 0.
Find the roots of the following quadratic equations, if they exist, by the method of completing the square 2x2 + x + 4 = 0
Find the roots of the quadratic equations 2x2 + x – 4 = 0 by applying the quadratic formula.
The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/h more than that of the passenger train, find the average speed of the two trains.
By using the method of completing the square, show that the equation `2x^2+x+4=0` has no real roots.
Fill in the gap and complete.

Fill in the gaps and complete.
If α, β are roots of quadratic equation,
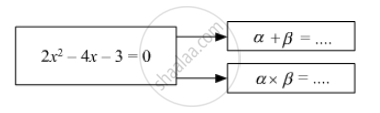
Find the value of discriminant.
2y2 – 5y + 10 = 0
A chess board contains 64 equal squares and the area of each square is 6.25 cm2. A border round the board is 2 cm wide. The length of the side of the chess board is:
