Advertisements
Advertisements
प्रश्न
Fill in the gaps and complete.
If α, β are roots of quadratic equation,
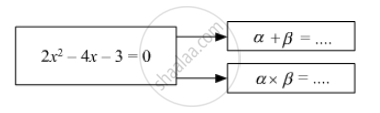
उत्तर
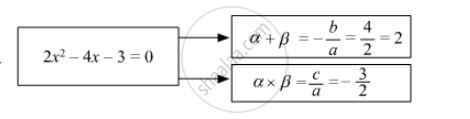
Sum of roots = \[\frac{- b}{a} = \frac{- \left( - 4 \right)}{2} = 2\]
Product of roots = \[\frac{c}{a} = \frac{- 3}{2}\]
APPEARS IN
संबंधित प्रश्न
Find the roots of the quadratic equation 4x2 + 4√3x + 3 = 0
Find the roots of the quadratic equation 2x2 + x + 4 = 0
Find the roots of the following quadratic equations, if they exist, by the method of completing the square 2x2 – 7x + 3 = 0
Find the roots of the quadratic equations `4x^2+4sqrt3x + 3 = 0` by applying the quadratic formula.
The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/h more than that of the passenger train, find the average speed of the two trains.
Find the roots of the following quadratic equations (if they exist) by the method of completing the square.
`sqrt2x^2-3x-2sqrt2=0`
The hypotenuse of a right=-angled triangle is 20 meters. If the difference between the lengths of the other sides be 4 meters, find the other sides
The ratio of the sum and product of the roots of the equation `7x^2-12x+18=0` is
(a) 7:12 (b)7:18 (c)3:2 (d)2:3
Solve the following quadratic equation by completing the square method.
9y2 – 12y + 2 = 0
Find the value of discriminant.
x2 + 7x – 1 = 0
Form the quadratic equation from the roots given below.
\[2 - \sqrt{5}, 2 + \sqrt{5}\]
Sum of the area of two squares is 400 cm2. If the difference of their perimeters is 16 cm, find the sides of two squares.
The sum of the areas of two squares is 400 sq.m. If the difference between their perimeters is 16 m, find the sides of two squares.
The sum of the squares of two consecutive natural numbers is 313. The numbers are:
The value of `sqrt(6 + sqrt(6 + sqrt(6 ....)))`
Find the remainder when p(x) = 3x2 + 2x – 7 is divided by 2x + 1.
Find the value of x, if `(4/7)^x (7/4)^(2x) = 343/64`.
Find the value of x, if `5^(x - 3) xx 5^(2x – 8)` = 625.
