Advertisements
Advertisements
प्रश्न
The sum of the areas of two squares is 400 sq.m. If the difference between their perimeters is 16 m, find the sides of two squares.
उत्तर
Let the sides of the two squares be x cm and y cm(x > y).
Then, their areas are x2 and y2 and their perimeters are 4x and 4y.
According to the first condition,
Sum of the areas of two squares is 400 sq.m
∴ x2 + y2 = 400 ........(i)
According to the second condition,
difference between the perimeters is 16 m
∴ 4x − 4y = 16
∴ 4(x − y) = 16
∴ x − y = 4
∴ x = y + 4
Substituting the value of x in equation (i), we get
(y + 4)2 + y2 = 400
∴ y2 + 8y + 16 + y2 = 400
∴ 2y2 + 8y – 384 = 0
∴ y2 + 4y – 192 = 0
∴ y2 + 16y – 12y – 192 = 0
∴ y(y + 16) – 12(y + 16) = 0
∴ (y + 16) (y – 12) = 0
∴ y + 16 = 0 or y – 12 = 0
∴ y = – 16 or y = 12
But, y ≠ – 16 as the side of a square cannot be negative.
∴ y = 12
∴ x = y + 4 = 12 + 4 = 16
∴ The sides of the two squares are 16 cm and 12 cm.
APPEARS IN
संबंधित प्रश्न
Find the roots of the quadratic equation 4x2 + 4√3x + 3 = 0
Find the roots of the quadratic equations 2x2 – 7x + 3 = 0 by applying the quadratic formula.
The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
Two water taps together can fill a tank in `9 3/8`hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Find the roots of the following quadratic equations (if they exist) by the method of completing the square.
`sqrt2x^2-3x-2sqrt2=0`
Find the roots of the following quadratic equations (if they exist) by the method of completing the square.
`sqrt3x^2+10x+7sqrt3=0`
`sqrt2x^3-3x-2sqrt2=0`
The length of a rectangle is thrice as long as the side of a square. The side of the square is 4 cm more than the width of the rectangle. Their areas being equal, find the dimensions.
Solve the following quadratic equation by completing the square method.
x2 + x – 20 = 0
Solve the following quadratic equation by completing the square method.
m2 – 5m = –3
Solve the following quadratic equation by completing the square method.
2y2 + 9y + 10 = 0
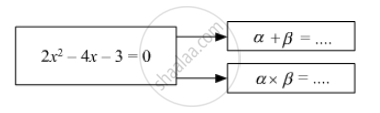
Fill in the gaps and complete.
If α, β are roots of quadratic equation,
Form the quadratic equation from the roots given below.
\[2 - \sqrt{5}, 2 + \sqrt{5}\]
α, β are roots of y2 – 2y –7 = 0 find,
α3 + β3
The difference of two natural numbers is 3 and the difference of their reciprocals is \[\frac{3}{28}\].Find the numbers.
A motor boat whose speed in still water is 18 km/hr takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream.
Sum of the area of two squares is 400 cm2. If the difference of their perimeters is 16 cm, find the sides of two squares.
If Ritu were younger by 5 years than what she really is, then the square of her age would have been 11 more than five times her present age. What is her present age?
