Advertisements
Advertisements
प्रश्न
Solve the following quadratic equation by completing the square method.
2y2 + 9y + 10 = 0
उत्तर
2y2 + 9y +10 = 0
`y^2 + 9/2y + 5 = 0` ...[Dividing both sides by 2]
If `y2 + 9/2y + k = (y + a)^2`, then
`y^2 + 9/2y + k = y^2 + 2ay + a^2`
Comparing the coefficients, we get
`9/2 = 2a and k = a^2`
∴ `a = 9/4 and k = (9/4)^2 = 81/16`
Now, `y^2 + 9/2y + 5 = 0`
∴ `y^2 + 9/2y + 81/16 - 81/16 + 5 = 0`
∴ `(y + 9/4)^2 + ((-81 + 80)/16) = 0`
∴ `(y + 9/4)^2 - 1/16 = 0`
∴ `(y + 9/4)^2 = 1/16`
Taking the square root of both sides, we get
`y + 9/4 = ± 1/4`
∴ `y + 9/4 = 1/4 or y + 9/4 = -1/4`
∴ `y = 1/4 - 9/4 or y = -1/4 - 9/4`
∴ `y = (-8)/4 = -2 or y = -10/4 = (-5)/2`
∴ The roots of the given quadratic equation are -2 and `(-5)/2`.
संबंधित प्रश्न
Find the roots of the following quadratic equations, if they exist, by the method of completing the square 2x2 + x + 4 = 0
Two water taps together can fill a tank in `9 3/8`hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Find the roots of the following quadratic equations (if they exist) by the method of completing the square.
`x^2-(sqrt2+1)x+sqrt2=0`
`x^2-(sqrt2+1)x+sqrt2=0`
By using the method of completing the square, show that the equation `2x^2+x+4=0` has no real roots.
The length of a rectangle is thrice as long as the side of a square. The side of the square is 4 cm more than the width of the rectangle. Their areas being equal, find the dimensions.
A farmer prepares rectangular vegetable garden of area 180 sq meters. With 39 meters of barbed wire, he can fence the three sides of the garden, leaving one of the longer sides unfenced. Find the dimensions of the garden.
Fill in the gap and complete.

Fill in the gaps and complete.
If α, β are roots of quadratic equation,
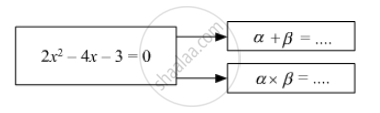
Form the quadratic equation from the roots given below.
0 and 4
α, β are roots of y2 – 2y –7 = 0 find,
α3 + β3
A motor boat whose speed in still water is 18 km/hr takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream.
Solve the following quadratic equation by completing square: z2 + 4z - 7 = 0.
For solving the quadratic equations `"x"^2 + 8"x" =-15` by completing the square method, find the third term.
One year ago, a man was 8 times as old as his son. Now his age is equal to the square of his son’s age. Their present ages are:
The value of `sqrt(6 + sqrt(6 + sqrt(6 ....)))`
If Ritu were younger by 5 years than what she really is, then the square of her age would have been 11 more than five times her present age. What is her present age?
Find the value of x, if `5^(x - 3) xx 5^(2x – 8)` = 625.
