Advertisements
Advertisements
प्रश्न
Find the sum of all 3-digit natural numbers, which are multiples of 11.
उत्तर
In the given problem, we need to find the sum of terms for different arithmetic progressions. So, here we use the following formula for the sum of n terms of an A.P.,
`S_n = n/2 [2a + (n - 1)d]`
Where; a = first term for the given A.P.
d = common difference of the given A.P.
n = number of terms
all 3-digit natural numbers, which are multiples of 11.
We know that the first 3 digit number multiple of 11 will be 110.
Last 3 digit number multiple of 11 will be 990.
So here,
First term (a) = 110
Last term (l) = 990
Common difference (d) = 11
So, here the first step is to find the total number of terms. Let us take the number of terms as n.
Now, as we know,
`a_n = a + (n - 1)d`
So for the last term
990 = 110 + (n -1) 11
990 = 110 + 11n - 11
990 = 99 + 11n
891 = 11n
81 = n
Now, using the formula for the sum of n terms, we get
`S_n = 81/2 [2(110) + (81 - 1)11]`
`S_n = 81/2 [220 + 80 xx 11]`
`S_n = 81/2 xx 1100`
`S_n = 81 xx 550`
`S_n = 44550`
Therefore, the sum of all the 3 digit multiples of 11 is 44550.
APPEARS IN
संबंधित प्रश्न
Check whether -150 is a term of the A.P. 11, 8, 5, 2, ....
Find the sum of first 51 terms of an AP whose second and third terms are 14 and 18 respectively.
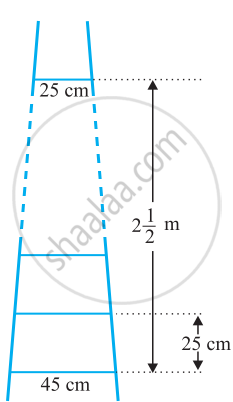
A ladder has rungs 25 cm apart. (See figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are 2 `1/2` m apart, what is the length of the wood required for the rungs?
[Hint: number of rungs = `250/25+ 1`]
Find the sum of n terms of an A.P. whose nth terms is given by an = 5 − 6n.
Find four numbers in AP whose sum is 8 and the sum of whose squares is 216.
The 9th term of an A.P. is equal to 6 times its second term. If its 5th term is 22, find the A.P.
If the sum of a certain number of terms starting from first term of an A.P. is 25, 22, 19, ..., is 116. Find the last term.
Q.6
Sum of 1 to n natural number is 45, then find the value of n.
