Advertisements
Advertisements
प्रश्न
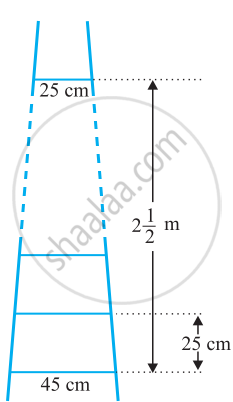
A ladder has rungs 25 cm apart. (See figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are 2 `1/2` m apart, what is the length of the wood required for the rungs?
[Hint: number of rungs = `250/25+ 1`]
उत्तर
It is given that the rungs are 25 cm apart and the top and bottom rungs are `2 1/2` m
Now, as the lengths of the rungs decrease uniformly, they will be in an A.P.
The length of the wood required for the rungs equals the sum of all the terms of this A.P.
First term, a = 45
Last term, l = 25
n = 11
Sn =` n/2(a+l)`
∴ S10 = `11/2(45+25`)
= `11/2 (70)`
= 385 cm
Therefore, the length of the wood required for the rungs is 385 cm.
APPEARS IN
संबंधित प्रश्न
In an AP given an = 4, d = 2, Sn = −14, find n and a.
In an AP given a = 3, n = 8, Sn = 192, find d.
Find the sum 3 + 11 + 19 + ... + 803
Find the sum of the first 15 terms of each of the following sequences having the nth term as
yn = 9 − 5n
Find the value of x for which the numbers (5x + 2), (4x - 1) and (x + 2) are in AP.
Find four numbers in AP whose sum is 8 and the sum of whose squares is 216.
If an denotes the nth term of the AP 2, 7, 12, 17, … find the value of (a30 - a20 ).
Find the sum of the following Aps:
i) 2, 7, 12, 17, ……. to 19 terms .
How many terms of the AP 63, 60, 57, 54, ….. must be taken so that their sum is 693? Explain the double answer.
The first term of an A. P. is 5 and the common difference is 4. Complete the following activity and find the sum of the first 12 terms of the A. P.
a = 5, d = 4, s12 = ?
`s_n = n/2 [ square ]`
`s_12 = 12/2 [10 +square]`
`= 6 × square `
` =square`
In an A.P. the first term is 8, nth term is 33 and the sum to first n terms is 123. Find n and d, the common differences.
Write the nth term of an A.P. the sum of whose n terms is Sn.
If `4/5` , a, 2 are three consecutive terms of an A.P., then find the value of a.
The number of terms of the A.P. 3, 7, 11, 15, ... to be taken so that the sum is 406 is
The sum of n terms of an A.P. is 3n2 + 5n, then 164 is its
Find the sum of first 20 terms of an A.P. whose first term is 3 and the last term is 57.
Find the common difference of an A.P. whose first term is 5 and the sum of first four terms is half the sum of next four terms.
Find second and third terms of an A.P. whose first term is – 2 and the common difference is – 2.
If Sn denotes the sum of first n terms of an AP, prove that S12 = 3(S8 – S4)
How many terms of the AP: –15, –13, –11,... are needed to make the sum –55? Explain the reason for double answer.
