Advertisements
Advertisements
प्रश्न
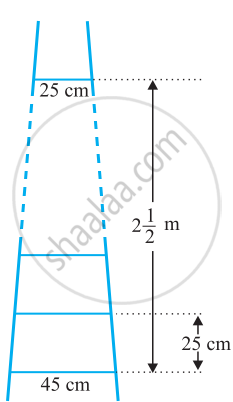
A ladder has rungs 25 cm apart. (See figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are 2 `1/2` m apart, what is the length of the wood required for the rungs?
[Hint: number of rungs = `250/25+ 1`]
उत्तर
It is given that the rungs are 25 cm apart and the top and bottom rungs are `2 1/2` m
Now, as the lengths of the rungs decrease uniformly, they will be in an A.P.
The length of the wood required for the rungs equals the sum of all the terms of this A.P.
First term, a = 45
Last term, l = 25
n = 11
Sn =` n/2(a+l)`
∴ S10 = `11/2(45+25`)
= `11/2 (70)`
= 385 cm
Therefore, the length of the wood required for the rungs is 385 cm.
APPEARS IN
संबंधित प्रश्न
Find the sum of all numbers from 50 to 350 which are divisible by 6. Hence find the 15th term of that A.P.
Check whether -150 is a term of the A.P. 11, 8, 5, 2, ....
A contract on a construction job specifies a penalty for delay of completion beyond a certain date as follows: Rs. 200 for the first day, Rs. 250 for the second day, Rs. 300 for the third day, etc., the penalty for each succeeding day being Rs. 50 more than for the preceding day. How much money does the contractor have to pay as a penalty if he has delayed the work by 30 days.
If (m + 1)th term of an A.P is twice the (n + 1)th term, prove that (3m + 1)th term is twice the (m + n + 1)th term.
Find the sum of 28 terms of an A.P. whose nth term is 8n – 5.
If the 10th term of an AP is 52 and 17th term is 20 more than its 13th term, find the AP
Find the middle term of the AP 6, 13, 20, …., 216.
Determine k so that (3k -2), (4k – 6) and (k +2) are three consecutive terms of an AP.
Write the next term for the AP` sqrt( 8), sqrt(18), sqrt(32),.........`
The nth term of an AP is given by (−4n + 15). Find the sum of first 20 terms of this AP?
Write an A.P. whose first term is a and common difference is d in the following.
The 19th term of an A.P. is equal to three times its sixth term. If its 9th term is 19, find the A.P.
Find the sum of all 2 - digit natural numbers divisible by 4.
The sum of first seven terms of an A.P. is 182. If its 4th and the 17th terms are in the ratio 1 : 5, find the A.P.
If the sum of three consecutive terms of an increasing A.P. is 51 and the product of the first and third of these terms is 273, then the third term is
The 9th term of an A.P. is 449 and 449th term is 9. The term which is equal to zero is
If k, 2k − 1 and 2k + 1 are three consecutive terms of an A.P., the value of k is
Suppose three parts of 207 are (a − d), a , (a + d) such that , (a + d) >a > (a − d).
Q.13
Find second and third terms of an A.P. whose first term is – 2 and the common difference is – 2.
