Advertisements
Advertisements
Question
A ladder has rungs 25 cm apart. (See figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are 2 `1/2` m apart, what is the length of the wood required for the rungs?
[Hint: number of rungs = `250/25+ 1`]
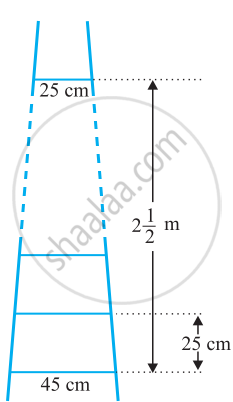
Solution
It is given that the rungs are 25 cm apart and the top and bottom rungs are `2 1/2` m
Now, as the lengths of the rungs decrease uniformly, they will be in an A.P.
The length of the wood required for the rungs equals the sum of all the terms of this A.P.
First term, a = 45
Last term, l = 25
n = 11
Sn =` n/2(a+l)`
∴ S10 = `11/2(45+25`)
= `11/2 (70)`
= 385 cm
Therefore, the length of the wood required for the rungs is 385 cm.
APPEARS IN
RELATED QUESTIONS
Find four numbers in A.P. whose sum is 20 and the sum of whose squares is 120
If the mth term of an A.P. is 1/n and the nth term is 1/m, show that the sum of mn terms is (mn + 1)
Find the sum of the following APs.
0.6, 1.7, 2.8, …….., to 100 terms.
How many terms of the A.P. 63, 60, 57, ... must be taken so that their sum is 693?
Find the sum of all odd natural numbers less than 50.
Find the sum of all natural numbers between 250 and 1000 which are divisible by 9.
The 24th term of an AP is twice its 10th term. Show that its 72nd term is 4 times its 15th term.
The sum of three numbers in AP is 3 and their product is -35. Find the numbers.
The first term of an AP is p and its common difference is q. Find its 10th term.
If ` 4/5 ` , a , 2 are in AP, find the value of a.
If (2p +1), 13, (5p -3) are in AP, find the value of p.
Write an A.P. whose first term is a and common difference is d in the following.
The 9th term of an A.P. is 449 and 449th term is 9. The term which is equal to zero is
If 18th and 11th term of an A.P. are in the ratio 3 : 2, then its 21st and 5th terms are in the ratio
The sum of first 14 terms of an A.P. is 1050 and its 14th term is 140. Find the 20th term.
Find the next 4 terms of the sequence `1/6, 1/4, 1/3`. Also find Sn.
Find the sum of the integers between 100 and 200 that are
- divisible by 9
- not divisible by 9
[Hint (ii) : These numbers will be : Total numbers – Total numbers divisible by 9]
Which term of the AP: –2, –7, –12,... will be –77? Find the sum of this AP upto the term –77.
Find the sum of first 16 terms of the A.P. whose nth term is given by an = 5n – 3.
Assertion (A): a, b, c are in A.P. if and only if 2b = a + c.
Reason (R): The sum of first n odd natural numbers is n2.
