Advertisements
Advertisements
प्रश्न
Find the derivatives from the left and from the right at x = 1 (if they exist) of the following functions. Are the functions differentiable at x = 1?
`f(x) = sqrt(1 - x^2)`
उत्तर
`f(x) = sqrt(1 - x^2)` at x = 1
To find the left limit of `f(x)` at x = 1
Put x = 1 – h
h > 0
When x → 1
We have h → 0
`f"'"(1 - "h") = lim_("h" -> 0) (f(1 - "h") - f(1))/(1 - "h" - 1)`
= `lim_("h" -> 0) (sqrt(1 - (1 - "h")^2) - sqrt(1 - 1^2))/(- "h")`
= `lim_("h" -> 0) (sqrt(1 - (1 - 2"h" + "h"^2)) - 0)/(- "h")`
= `lim_("h" -> 0) sqrt(1 + 1 + 2"h" - "h"^2)/(- "h")`
= `lim_("h" -> 0) sqrt("h"^2 (2/"h" - 1))/(- "h")`
= `lim_("h" -> 0) ("h" sqrt(2/"h" - 1))/(- "h")`
= `- lim_("h" -> 0) sqrt(2/"h" - 1)`
`f"'" (1^-) = - sqrt(2/0 - 1) = - sqrt(oo - 1)`
`f"'"(1^-) = - oo` .........(1)
To find the right limit of `f(x)` at x = 1
Put x = 1 + h
h > 0
When x → 1
We have h → 0
`f"'"(1 + "h") = lim_("h" -> 0) (f(1 + "h") - f(1))/(1 + "h" - 1)`
= `lim_("h" -> 0) (sqrt(1 - (1 + "h")^2) - sqrt(1 - 1^2))/"h"`
= `lim_("h" -> 0) sqrt(1 - (1 + 2"h" + "h"^2))/"h"`
= `lim_("h" -> 0) sqrt(1 - 1 - 2"h" - "h"^2)/"h"`
= `lim_("h" -> 0) sqrt(- "h"^2(1 + 2/"h"))/"h"`
= `lim_("h" -> 0) (sqrt(- 1) * "h")/"h" * sqrt(1 + 2/"h")`
= `lim_(h' -> 0) "i" * sqrt(1 + 2/"h")`
`f"'"(1^+) = "i" sqrt(1 + 2/0) = "i" xx oo` .......(2)
From equations (1) and (2) we get
`f"'"(1^-) ≠ f"'"(1^+)`
∴ `f"'"(x)` does not exist at x = 1
Hence `f(x) = sqrt(1 - x^2)` is n differentiable at x = 1.
APPEARS IN
संबंधित प्रश्न
Find the derivatives of the following functions using first principle.
f(x) = – 4x + 7
Find the derivatives of the following functions using first principle.
f(x) = – x2 + 2
Find the derivatives from the left and from the right at x = 1 (if they exist) of the following functions. Are the functions differentiable at x = 1?
`f(x) = {{:(x",", x ≤ 1),(x^2",", x > 1):}`
Show that the following functions are not differentiable at the indicated value of x.
`f(x) = {{:(3x",", x < 0),(-4x",", x ≥ 0):}` , x = 0
The graph of f is shown below. State with reasons that x values (the numbers), at which f is not differentiable.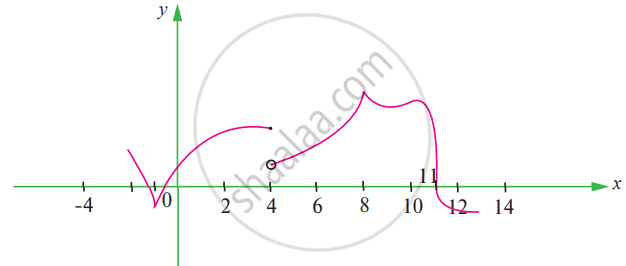
Examine the differentiability of functions in R by drawing the diagram
|sin x|
Choose the correct alternative:
f y = f(x2 + 2) and f'(3) = 5 , then `("d"y)/("d"x)` at x = 1 is
Choose the correct alternative:
If f(x) = x2 – 3x, then the points at which f(x) = f’(x) are
Choose the correct alternative:
If y = mx + c and f(0) = f’(0) = 1, then f(2) is
Choose the correct alternative:
If f(x) = x + 2, then f'(f(x)) at x = 4 is
Choose the correct alternative:
If pv = 81, then `"dp"/"dv"` at v = 9 is
Choose the correct alternative:
It is given that f'(a) exists, then `lim_(x -> "a") (xf("a") - "a"f(x))/(x - "a")` is
Choose the correct alternative:
If f(x) = `{{:(x + 1, "when" x < 2),(2x - 1, "when" x ≥ 2):}` , then f'(2) is
Choose the correct alternative:
If f(x) = `{{:(x + 2, - 1 < x < 3),(5, x = 3),(8 - x, x > 3):}` , then at x = 3, f'(x) is
