Advertisements
Advertisements
प्रश्न
Find the greatest number that will divide 445, 572 and 699, leaving remainders 4, 5, 6 respectively.
उत्तर
Since the respective remainders of 445, 572, and 699 are 4, 5, and 6, we have to find the number which exactly divides (445-4), (572-5), and (696-6).
So, the required number is the HCF of 441, 567, and 693.
Firstly, we will find the HCF of 441 and 567.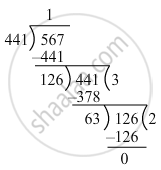
∴ HCF = 63
Now, we will find the HCF of 63 and 693.
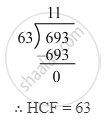
∴ HCF = 63
Hence, the required number is 63.
APPEARS IN
संबंधित प्रश्न
Test the divisibility of the following number by 3:
79124
Test the divisibility of the following number by 4:
946126
Test the divisibility of the following numbers by 5:
35208
Test the divisibility of the following numbers by 8:
1790184
Test the divisibility of the following numbers by 9:
647514
Test the divisibility of the following number by 10:
5790
Test the divisibility of the following number by 11:
83721
In the following number, replace * by the smallest number to make it divisible by 11:
467*91
Test the divisibility of 12030624 by 8.
State if the following is a prime number?
217
