Advertisements
Advertisements
Question
Find the greatest number that will divide 445, 572 and 699, leaving remainders 4, 5, 6 respectively.
Solution
Since the respective remainders of 445, 572, and 699 are 4, 5, and 6, we have to find the number which exactly divides (445-4), (572-5), and (696-6).
So, the required number is the HCF of 441, 567, and 693.
Firstly, we will find the HCF of 441 and 567.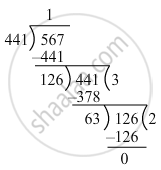
∴ HCF = 63
Now, we will find the HCF of 63 and 693.
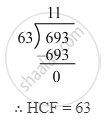
∴ HCF = 63
Hence, the required number is 63.
APPEARS IN
RELATED QUESTIONS
Test the divisibility of the following number by 2:
357986
Test the divisibility of the following number by 3:
733
Test the divisibility of the following numbers by 6:
46523
Test the divisibility of the following numbers by 7:
2345
In the following number, replace * by the smallest number to make it divisible by 3:
8*711
Test the divisibility of 10001001 by 3.
Write (T) for true and (F) for false against the following statement:
If a number is divisible by both 9 and 10, it must be divisible by 90.
Find the greatest number which divides 2011 and 2623, leaving remainders 9 and 5 respectively.
Which of the following numbers is divisible by 4?
On dividing 5035 by 31, the remainder is 13. Find the quotient.
