Question

Find the image of the point (1, 2, 1) with respect to the line `(x - 3)/(1) = (y + 1)/(2) = (z - 1)/3`. Also find the equation of the line joining the given point and its image.

Answer 1

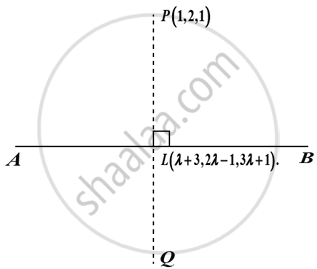
Let P(1, 2, 1) be the given point and L be the foot of the perpendicular from P to the given line AB (as shown in the figure above).

Let’s put `(x - 3)/(1) = (y + 1)/(2) = (z - 1)/(3) = lambda`. Then, x = λ + 3, y = 2λ − 1, z = 3λ + 1.

Let the coordinates of the point L be (λ + 3, 2λ − 1, 3λ + 1).

So, direction ratios of  PL are (λ + 3 − 1, 2λ − 1 − 2, 3λ + 1 − 1), i.e., (λ + 2, 2λ − 3, 3λ)

Direction ratios of the given line are 1, 2 and 3, which is perpendicular to PL. Therefore, we have,

`(lambda + 2)*1 + (2lambda - 3)*2 + 3lambda*3 = 0 ⇒ 14lambda = 4 ⇒ lambda = 2/7` 

Then, `lambda + 3 = 2/7 + 3 = 23/7; 2lambda -1 = 2(2/7) - 1 = -3/7;  3lambda + 1 = 3(2/7) + 1 = 13/7`

Therefore, coordinates of the point L are `(23/7, -3/7, 13/7)`.

Let Q(x₁, y₁, z₁) be the image of P(1, 2, 1) with respect to the given line. Then, L is the mid-point of PQ.

Therefore, `(1 + x_1)/(2) = (23)/(7), (2 + y_1)/(2) = -3/7, (1 + z_1)/(2) = 13/7 ⇒ x _1 = 39/7, y_1 = -20/7, z_1 = 19/7`

Hence, the image of the point P(1, 2, 1) with respect to the given line Q `(39/7, -20/7, 19/7)`.

The equation of the line joining P(1, 2, 1) and Q `(39/7, -20/7, 19/7)  "is"  (x - 1)/(32//7) = (y - 2)/(-34//7) = (z - 1)/(12//7) ⇒ (x - 1)/16 = (y - 2)/-17 = (z - 1)/6`.