Mathematics Board Sample Paper 2024-2025 Commerce (English Medium) Class 12 Question Paper Solution

If for a square matrix A, A. (adj A) = `[(2025, 0, 0),(0, 2025, 0),(0, 0, 2025)]`, then the value of |A|+ |adj A| is equal to ______.

1

2025 + 1

(2025)² + 45

2025 + (2025)²

Assume X, Y, Z, W and P are matrices of order 2 × n, 3 × k, 2 × p, n × 3 and p × k, respectively.

The restrictions on n, k and p so that PY + WY will be defined are ______.

k = 3, p = n

k is arbitrary, p = 2

p is arbitrary, k = 3

k = 2, p = 3

The interval in which the function f defined by f(x) = e^x is strictly increasing is ______.

(1, ∞)

(−∞, 0)

(−∞, ∞)

(0, ∞)

If A and B are non-singular matrices of same order with det(A) = 5, then det(B⁻¹AB)² is equal to ______.

5

5²

5⁴

5⁵

The value of  'n', such that the differential equation `x^ndy/dx = y(logy - logx + 1)`; (where x, y ∈ R⁺) is homogeneous, is ______.

0

1

2

3

If the points (x₁, y₁), (x₂, y₂) and (x₁ + x₂, y₁ + y₂) are collinear, then x₁y₂ is equal to ______.

x₂y₁

x₁y₁

x₂y₂

x₁x₂

If A = `[(0, 1, c), (-1, a, -b), (2, 3, 0)]` is a skew-symmetric matrix, then the value of a + b + c = ______.

1

2

3

4

For any two events A and B, if `P(barA) = 1/2, P(barB) = 2/3  "and" P(A\capB) = 1/4, "then" P(barA//barB)` equals ______.

`3/8`

`8/9`

`5/8`

`1/4`

The value of α if the angle between `overset->p = 2alpha^2hati - 3alphahatj + hatk and overset->q = hati + hatj + alphahatk`  is obtuse is ______.

R − [0, 1]

(0, 1)

[0, ∞)

[1, ∞)

If `|overset->a|` = 3, `|overset->b|` = 4 and `|overset->a + overset->b|` = 5, then `|overset->a - overset->b|` = ______.

3

4

5

8

For the linear programming problem (LPP), the objective function is Z = 4x + 3y and the feasible region determined by a set of constraints is shown in the graph:

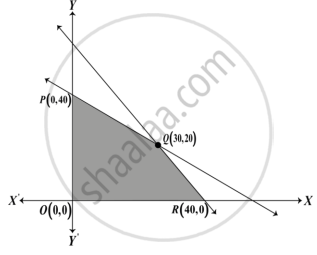
Which of the following statements is true?

Maximum value of Z is at R(40, 0).

Maximum value of Z is at Q(30, 20).

Value of Z is at R(40, 0) is less than the value at P(0, 40).

Value of Z is at Q(30, 20) is less than the value at R(40, 0).

`intdx/(x^3(1 + x^4)^(1/2))` equals ______.

`-1/(2x^2) sqrt(1 + x^4) + c`

`1/(2x) sqrt(1 + x^4) + c`

`-1/(4x) sqrt(1 + x^4) + c`

`1/(4x^2) sqrt(1 + x^4) + c`

`int_0^(2pi) cosec^7xdx` = ______

0

1

4

2π

What is the general solution of the differential equation `e^(y') = x`?

y = xlogx + c

y = xlogx − x + c

y = xlogx + x + c

y = x + c

The graph drawn below depicts:

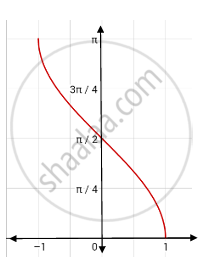
y = sin⁻¹x

y = cos⁻¹x

y = cosec⁻¹x

y = cot⁻¹x

A linear programming problem (LPP) along with the graph of its constraints is shown below.

The corresponding objective function is Z = 18x + 10y, which has to be minimized. The smallest value of the objective function Z is 134 and is obtained at the corner point (3, 8).

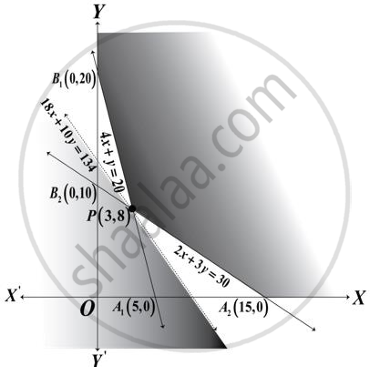
The optimal solution of the above linear programming problem:

Does not exist as the feasible region is unbounded.

Does not exist as the inequality 18x + 10y < 134 does not have any point in common with the feasible region.

Exists as the inequality 18x + 10y > 134 has infinitely many points in common with the feasible region.

Exists as the inequality 18x + 10y < 134 does not have any point in common with the feasible region.

The function f : R → Z defined by f(x) = [x]; where [.] denotes the greatest integer function, is ______.

Continuous at x = 2.5 but not differentiable at x = 2.5

Not Continuous at x = 2.5 but differentiable at x = 2.5

Not Continuous at x = 2.5 and not differentiable at x = 2.5

Continuous as well as differentiable at x = 2.5

A student observes an open-air Honeybee nest on the branch of a tree, whose plane figure is parabolic shape given by x² = 4y. Then the area (in sq units) of the region bounded by parabola x² = 4y and the line y = 4 is ______.

`32/3`

`64/3`

`128/3`

`256/3`

Assertion (A): Consider the function defined as f(x) = |x| + |x − 1|, x ∈ R. Then f(x) is not differentiable at x = 0 and x = 1.

Reason (R): Suppose f be defined and continuous on (a, b) and c ∈ (a, b), then f(x) is not differentiable at x = c if `lim_(h->0^-) (f(c + h) - f(c))/(h) ne lim_(h->0^+) (f(c + h) - f(c))/(h)`.

Both (A) and (R) are true and (R) is the correct explanation of (A).

Both (A) and (R) are true but (R) is not the correct explanation of (A).

(A) is true but (R) is false.

(A) is false but (R) is true.

Assertion (A): The function `f : R  - {(2n + 1) pi/2 : n in Z} -> (- infty, -1] cup [1, infty)` defined by f(x) = sec x is not one-one function in its domain.

Reason (R): The line y = 2 meets the graph of the function at more than one point.

Both (A) and (R) are true and (R) is the correct explanation of (A).

Both (A) and (R) are true but (R) is not the correct explanation of (A).

(A) is true but (R) is false.

(A) is false but (R) is true.

If `cot^-1(3x + 5)> pi/4`, then find the range of the values of x.

The cost (in rupees) of producing x items in the factory each day is given by C(x) = 0.00013x³ + 0.002x² + 5x + 2000.

Find the marginal cost when 150 items are produced.

Find the derivative of tan⁻¹ x with respect to logx; (where x ∈ (1, ∞)).

Differentiate the following function with respect to x:

`(cos x)^x; ("where"  x in (0,  pi/2))`

If vectors `overset->a = 2hati + 2hatj + 3hatk,  overset->b = -hati + 2hatj + hatk and overset->c = 3hati + hatj` are such that `overset->b  + lambda overset->c`  is perpendicular to `overset->a`, then find the value of λ.

A person standing at O(0, 0, 0) is watching an aeroplane which is at the coordinate point A(4, 0, 3). At the same time, he saw a bird at the coordinate point B(0, 0, 1). Find the angles which `overset->(BA)` makes with the x, y and z axes.

The two co-initial adjacent sides of a parallelogram are `2hati - 4hatj - 5hatk and 2hati + 2hatj + 3hatk`. Find its diagonals and use them to find the area of the parallelogram.

A kite is flying at a height of 3 metres and 5 metres of string is out. If the kite is moving away horizontally at the rate of 200 cm/s, find the rate at which the string is being released.

According to a psychologist, the ability of a person to understand spatial concepts is given by `A = 1/3sqrtt`, where t is the age in years, t ∈ [5, 18]. Show that the rate of increase of the ability to understand spatial concepts decreases with age in between 5 and 18.

An ant is moving along the vector `overset->l_1 = hati - 2hatj + 3hatk`. Few sugar crystals are kept along the vector `overset->l_2 = 3hati - 2hatj + hatk` which is inclined at an angle θ with the vector `overset->l_1`. Then find the angle θ. Also find the scalar projection of `overset->l_1  "on"  overset->l_2`.

Find the vector and the cartesian equation of the line that passes through (−1, 2, 7) and is perpendicular to the lines `overset->r = 2hati + hatj -3hatk + lambda(hati + 2hatj + 5hatk)` and `overset->r = 3hati + 3hatj - 7hatk + mu(3hati - 2hatj + 5hatk)`.

Evaluate:

`int{1/logx - 1/(logx)^2}dx`; (where x > 1).

Evaluate:

`int_0^1x(1 - x)^ndx`; (where n ∈ N).

Solve the following Linear Programming Problems graphically:

Minimise Z = x + 2y

subject to 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0.

The probability that it rains today is 0.4. If it rains today, the probability that it will rain tomorrow is 0.8. If it does not rain today, the probability that it will rain tomorrow is 0.7. If

P₁: denotes the probability that it does not rain today.

P₂: denotes the probability that it will not rain tomorrow if it rains today.

P₃: denotes the probability that it will rain tomorrow if it does not rain today.

P₄: denotes the probability that it will not rain tomorrow if it does not rain today.

1. Find the value of P₁ × P₄ − P₂ × P₃.
2. Calculate the probability of it raining tomorrow.

A random variable X can take all non-negative integral values and the probability that X takes the value r is proportional to 5^−𝑟. Find P (X < 3).

Draw the rough sketch of the curve y = 20 cos2x; `("where"  pi/6 ≤ x ≤ pi/3)`.

Using integration, find the area of the region bounded by the curve y = 20 cos2x from the coordinates `x = pi/6` to `x = pi/3` and the x-axis.

The equation of the path traversed by the ball headed by the footballer is y = ax² + bx + c (where 0 ≤ x ≤ 14 and  and a, b, c ∈ R and a ≠ 0) with respect to a XY-coordinate system in the vertical plane. The ball passes through the points (2, 15), (4, 25) and (14, 15). Determine the values of a, b and c by solving the system of linear equations in a, b and c using the matrix method. Also find the equation of the path traversed by the ball.

If f : R → R is defined by f(x) = |x|³, show that f''(x) exists for all real x and find it.

If (x − a)² + (y − b)² = c², for some c > 0, prove that `([1 + (dy/dx)^2]^(3/2))/((d^2y)/dx^2)` is a constant independent of a and b.

Find the shortest distance between the lines l₁ and l₂ whose vector equations are `overset->r = (-hati -hatj -hatk) + lambda(7hati - 6hatj + hatk)  "and"  overset->r = (3hati + 5hatj + 7hatk) + mu(hati - 2hatj +hatk)` where λ and μ are parameters.

Find the image of the point (1, 2, 1) with respect to the line `(x - 3)/(1) = (y + 1)/(2) = (z - 1)/3`. Also find the equation of the line joining the given point and its image.

Based on the above information, answer the following questions:

1. Express the volume (V) of each container as function of x only.  (1)
2. Find `(dV)/dx`.  (1)
3.    
   1. For what value of x, the volume of each container is maximum?  (2)
                               OR
   2. Check whether V has a point of inflection at x = `65/6` or not?  (2)

On the basis of the above information, answer the following questions:

1. Ravi wishes to form all the relations possible from B to G. How many such relations are possible?  (1)
2. Write the smallest equivalence relation on G.  (1)
3.    
   1. Ravi defines a relation from B to B as R₁ = {(b₁, b₂), (b₂, b₁)}. Write the minimum ordered pairs to be added in R₁ so that it becomes 
      1. reflexive but not symmetric,
      2. reflexive and symmetric but not transitive.  (2)
                               OR
   2. If the track of the final race (for the biker b₁) follows the curve
      `x^2 = 4y; ("where"  0 ≤ x ≤ 20sqrt2   "and"  0 ≤ y ≤ 200)`, then state whether the track represents a one-one and onto function or not. (Justify).  (2)

On the basis of the above information, answer the following questions:

1. When two birds flew from Cage-I to Cage-II and two birds flew back from Cage-II to Cage-I, then find the probability that the owl is still in Cage-I.  (2)
2. When two birds flew from Cage-I to Cage-II and two birds flew back from Cage-II to Cage-I, the owl is still seen in Cage-I. What is the probability that one parrot and the owl flew from Cage-I to Cage-II?  (2)