Advertisements
Advertisements
प्रश्न
Find the LCM and HCF of the following integers by applying the prime factorisation method.
8, 9 and 25
उत्तर
 |
 |
 |
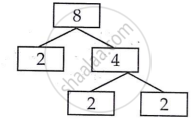
8 = 2 × 2 × 2
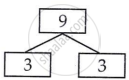
9 = 3 × 3
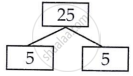
25 = 5 × 5
L.C.M of 8, 9 and 25 = `2^2xx3^2xx5^2`
L.C.M of 8, 9 and 25 = 1800
H.C.F of 8, 9 and 25 = 1
संबंधित प्रश्न
Consider the number 6n where n is a natural number. Check whether there is any value of n ∈ N for which 6n is divisible by 7.
Given that HCF (306, 657) = 9, find LCM (306, 657).
There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?
Find HCF and LCM of 404 and 96 and verify that HCF × LCM = Product of the two given numbers.
State fundamental theorem of arithmetic?
Determine the prime factorisation of each of the following positive integer:
58500
Find the LCM and HCF of the following integers by applying the prime factorisation method:
24, 15 and 36
Write down the decimal expansions of the following rational numbers by writing their denominators in the form 2m × 5n, where, m, n are non-negative integers.\[\frac{129}{2^2 \times 5^7}\]
Write the exponent of 2 in the price factorization of 144.
If the prime factorization of a natural number n is 23 ✕ 32 ✕ 52 ✕ 7, write the number of consecutive zeros in n.
Find the H.C.F. of 252525 and 363636
If 13824 = 2a × 3b then find a and b
Express 98 as a product of its primes.
If two positive integers A and B can be expressed as A = xy3 and B = xiy2z; x, y being prime numbers, the LCM (A, B) is ______.
According to the fundamental theorem of arithmetic, if T (a prime number) divides b2, b > 0, then ______.
For some integer q, every odd integer is of the form ______.
If the HCF of 65 and 117 is expressible in the form 65m – 117, then the value of m is ______.
If two positive integers p and q can be expressed as p = ab2 and q = a3b; a, b being prime numbers, then LCM (p, q) is ______.
The LCM of smallest 2-digit number and smallest composite number is ______.
If HCF (72, 120) = 24, then LCM (72, 120) is ______.
