Advertisements
Advertisements
प्रश्न
There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?
उत्तर
Since they both move in the same direction and at the same time, to find the time when will they both meet together again, it is enough if we find the LCM of 12 and 18
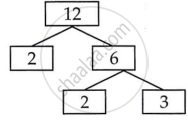 |
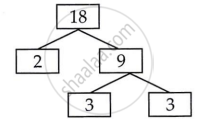 |
12 = 2 × 2 × 3
18 = 2 × 3 × 3
LCM (18, 12) = 2 × 2 × 3 × 3 = 36
Therefore, Sonia and Ravi will meet again after 36 minutes.
APPEARS IN
संबंधित प्रश्न
Check whether 6n can end with the digit 0 for any natural number n.
A merchant has 120 liters of oil of one kind, 180 liters of another kind and 240 liters of third kind. He wants to sell the oil by filling the three kinds of oil in tins of equal capacity. What should be the greatest capacity of such a tin?
Find the LCM and HCF of the following integers by applying the prime factorisation method:
24, 15 and 36
The HCF of two numbers is 145 and their LCM is 2175. If one number is 725, find the other.
Write down the decimal expansions of the following rational numbers by writing their denominators in the form 2m × 5n, where, m, n are non-negative integers. \[\frac{3}{8}\]
Write the sum of the exponents of prime factors in the prime factorization of 98.
If m, n are natural numbers, for what values of m, does 2n × 5m ends in 5?
If p1x1 × p2x2 × p3x3 × p4x4 = 113400 where p1, p2, p3, p4 are primes in ascending order and x1, x2, x3, x4, are integers, find the value of p1, p2, p3, p4 and x1, x2, x3, x4
Find the greatest number consisting of 6 digits which is exactly divisible by 24, 15, 36?
Find the least positive value of x such that 89 ≡ (x + 3) (mod 4)
The sum of the exponents of the prime factors in the prime factorization of 1729 is
For some integer p, every even integer is of the form ______.
If LCM(x, 18) = 36 and HCF(x, 18) = 2, then x is ______.
For some integer m, every even integer is of the form ______.
If the HCF of 65 and 117 is expressible in the form 65m – 117, then the value of m is ______.
The largest number which divides 70 and 125, leaving remainders 5 and 8, respectively, is ______.
If two positive integers a and b are written as a = x3 y2 and b = xy3; x, y are prime numbers, then HCF (a, b) is ______.
Show the 6n cannot end with digit 0 for any natural number 'n'.
The LCM of smallest 2-digit number and smallest composite number is ______.
Assertion (A): The HCF of two numbers is 5 and their product is 150. Then their LCM is 40.
Reason(R): For any two positive integers a and b, HCF (a, b) × LCM (a, b) = a × b.
