Advertisements
Advertisements
प्रश्न
Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius r units.
उत्तर
Radius of a cone = Radius of a hemisphere = r unit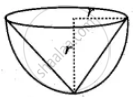
Height of a cone = r units
(height of the cone = radius of a hemisphere)
Maximum volume of the cone
= `1/3 pi"r"^2` cu.unis
= `1/3pi"r"^2 xx "r"` cu.units
= `1/3 pi"r"^3` cu.units
Maximum volume ofthe cone
= `1/3 pi"r"^3` cu.units
APPEARS IN
संबंधित प्रश्न
Find the amount of water displaced by a solid spherical ball of diameter 28 cm.
`["Assume "pi=22/7]`
Find the volume of a sphere whose diameter is 2.1 m .
A sphere of radius 5 cm is immersed in water filled in a cylinder, the level of water rises `5/3`cm. Find the radius of the cylinder.
The diameter of a coper sphere is 18 cm. The sphere is melted and is drawn into a long wire of uniform circular cross-section. If the length of the wire is 108 m, find its diameter.
A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine `("in " mm^3)` is needed to fill this capsule?
A solid sphere and a solid hemisphere have an equal total surface area. Prove that the ratio of their volume is `3sqrt(3):4`
A spherical ball of radius r1 units is melted to make 8 new identical balls each of radius r2 units. Then r1 : r2 is
If a sphere is inscribed in a cube, then the ratio of the volume of the cube to the volume of the sphere will be 6 : π.
Metal spheres, each of radius 2 cm, are packed into a rectangular box of internal dimensions 16 cm × 8 cm × 8 cm. When 16 spheres are packed the box is filled with preservative liquid. Find the volume of this liquid. Give your answer to the nearest integer. [Use π = 3.14]
A cube of side 4 cm contains a sphere touching its sides. Find the volume of the gap in between.
