Advertisements
Advertisements
Question
Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius r units.
Solution
Radius of a cone = Radius of a hemisphere = r unit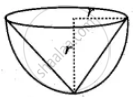
Height of a cone = r units
(height of the cone = radius of a hemisphere)
Maximum volume of the cone
= `1/3 pi"r"^2` cu.unis
= `1/3pi"r"^2 xx "r"` cu.units
= `1/3 pi"r"^3` cu.units
Maximum volume ofthe cone
= `1/3 pi"r"^3` cu.units
APPEARS IN
RELATED QUESTIONS
Find the volume of a sphere whose radius is 0.63 m.
`["Assume "pi=22/7]`
Find the amount of water displaced by a solid spherical ball of diameter 0.21 m.
`["Assume "pi=22/7]`
A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1 m, then find the volume of the iron used to make the tank.
`["Assume "pi=22/7]`
A hemispherical tank has inner radius of 2.8 m. Find its capacity in litres.
A cylinder of radius 12 cm contains water to a depth of 20 cm. A spherical iron ball is dropped into the cylinder and thus the level of water is raised by 6.75 cm. Find the radius of the ball.
(Use 𝜋 = 22/7).
A metallic sphere of radius 10.5 cm is melted and thus recast into small cones, each of radius 3.5 cm and height 3 cm. Find how many cones are obtained.
If the ratio of radii of two spheres is 4 : 7, find the ratio of their volumes.
The number of planks of dimensions (4 m × 50 cm × 20 cm) that can be stored in a pit which is 16 m long, 12 m wide and 4 m deep is ______.
Two solid spheres made of the same metal have weights 5920 g and 740 g, respectively. Determine the radius of the larger sphere, if the diameter of the smaller one is 5 cm.
The volumes of the two spheres are in the ratio 64 : 27. Find the ratio of their surface areas.
