Advertisements
Advertisements
प्रश्न
Find the slope of the line passing through the points A(4,7) and B(2,3).
उत्तर
A ≡ (4,7) ≡ (x1, y1) and B ≡ (2,3) ≡ (x2, y2)
`"Slope of line AB "=(("y"_2-"y"_1))/(("x"_2-"x"_1))=(3-7)/(2-4)=(-4)/-2=2`
APPEARS IN
संबंधित प्रश्न
A slope of a line is 3 and y-intercept is –4. Write the equation of a line
The side AB of a square ABCD is parallel to the x-axis. Find the slopes of all its sides. Also, find:
- the slope of the diagonal AC.
- the slope of the diagonal BD.
Determine x so that the slope of the line through (1, 4) and (x, 2) is 2.
Find the slope of the line which is parallel to `x/2 - y/3 -1 = 0 `
Lines mx + 3y + 7 = 0 and 5x – ny – 3 = 0 are perpendicular to each other. Find the relation connecting m and n.
If the lines y = 3x + 7 and 2y + px = 3 are perpendicular to each other, find the value of p.
The line through A(−2, 3) and B(4, b) is perpendicular to the line 2x – 4y = 5. Find the value of b.
The ordinate of a point lying on the line joining the points (6, 4) and (7, –5) is –23. Find the coordinates of that point.
Find the slope of the lines passing through the given point.
E(–4, –2) , F (6, 3)
Find k, if B(k, –5), C (1, 2) and slope of the line is 7.
Find the slope of a line, correct of two decimals, whose inclination is 50°
Find the slope of a line parallel to the given line 5x-y = 10
Find m if the slope of the line passing through the point (-7,5) and (2,m) is `1/3`
Verify whether the following points are collinear or not:
A(1, –3), B(2, –5), C(–4, 7).
Find the slope of the line passing through the points M(4,0) and N(-2,-3).
If A(6, 1), B(8, 2), C(9, 4) and D(7, 3) are the vertices of `square`ABCD, show that `square`ABCD is a parallelogram.
Solution:
Slope of line = `("y"_2 - "y"_1)/("x"_2 - "x"_1)`
∴ Slope of line AB = `(2 - 1)/(8 - 6) = square` .......(i)
∴ Slope of line BC = `(4 - 2)/(9 - 8) = square` .....(ii)
∴ Slope of line CD = `(3 - 4)/(7 - 9) = square` .....(iii)
∴ Slope of line DA = `(3 - 1)/(7 - 6) = square` .....(iv)
∴ Slope of line AB = `square` ......[From (i) and (iii)]
∴ line AB || line CD
∴ Slope of line BC = `square` ......[From (ii) and (iv)]
∴ line BC || line DA
Both the pairs of opposite sides of the quadrilateral are parallel.
∴ `square`ABCD is a parallelogram.
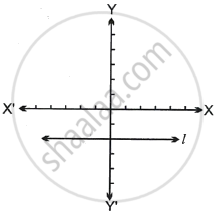
In the figure, line l is parallel to X-axis. Which of the following statement is true?