Advertisements
Advertisements
प्रश्न
Find the third proportional to `x/y + y/x` and `sqrt(x^2 + y^2)`
उत्तर
Let the required third proportional be p.
`=> x/y + y/x, sqrt(x^2 + y^2)`, p are in continued proportion
`=> x/y + y/x : sqrt(x^2 + y^2) = sqrt(x^2 + y^2) : p`
`=> p(x/y + y/x) = (sqrt(x^2 + y^2))^2`
`=> p((x^2 + y^2)/(xy)) = x^2 + y^2`
`=>` p = xy
APPEARS IN
संबंधित प्रश्न
If x, y, z are in continued proportion, prove that `(x + y)^2/(y + z)^2 = x/z`
Find the mean proportion of the following :
`28/3` and `175/27`
If u, v, w, and x are in continued proportion, then prove that (2u+3x) : (3u+4x) : : (2u3+3v3) : (3u3+4v3)
`("pqr")^2 (1/"p"^4 + 1/"q"^4 + 1/"r"^4) = ("p"^4 + "q"^4 + "r"^4)/"q"^2`
Find the third proportional to Rs. 3, Rs. 12
If b is the mean proportional between a and c, prove that (ab + bc) is the mean proportional between (a² + b²) and (b² + c²).
If ax = by = cz; prove that `x^2/"yz" + y^2/"zx" + z^2/"xy" = "bc"/a^2 + "ca"/b^2 + "ab"/c^2`
If a, b, c, d are in continued proportion, prove that: `(a^3 + b^3 + c^3)/(b^3 + c^3 + d^3) = a/d`
7 Persons is to 49 Persons as 11 kg is to 88 kg
Fill the boxes using any set of suitable numbers 6 : `square` : : `square` : 15
Sleeping time of a python in a 24 hour clock is represented by the shaded portion in figure.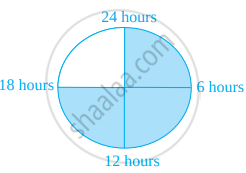
The ratio of sleeping time to awaking time is ______.
