Advertisements
Advertisements
प्रश्न
Find the value of k such that the polynomial x2 − (k + 6)x + 2(2k −1) has sum of its zeros equal to half of their product.
उत्तर
Given polynomial is x2 - (k + 6) x + 2 (2k – 1)
Here
a = 1, b = - (k + 6), c = 2 (2k – 1)
Given that,
Sum of zeroes = `(1)/(2)` product of zeroes
⇒ `[-[-("k"+6)]]/(1) = (1)/(2) xx (2(2"k" - 1))/(1)`
⇒ `"k" + 6 = 2"k" - 1`
⇒ `6 + 1 = 2"k" - "k"`
⇒ `"k" = 7`
APPEARS IN
संबंधित प्रश्न
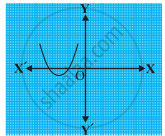
The graphs of y = p(x) are given in following figure, for some polynomials p(x). Find the number of zeroes of p(x).
Find all the zeroes of `(2x^4 – 3x^3 – 5x2 + 9x – 3)`, it is being given that two of its zeroes are `sqrt3 and –sqrt3`.
Find the zeroes of the polynomial `x^2 – 3x – m(m + 3)`
If 3 is a zero of the polynomial `2x^2 + x + k`, find the value of k.
Write the zeros of the polynomial `f(x) = x^2 – x – 6`.
Find the zeroes of the quadratic polynomial `f(x) = 4sqrt3x^2 + 5x – 2sqrt3`.
If one of the zeroes of the quadratic polynomial (k – 1) x2 + kx + 1 is - 3, then the value of k is ______.
If the zeroes of the quadratic polynomial x2 + (a + 1) x + b are 2 and –3, then ______.
If the graph of a polynomial intersects the x-axis at exactly two points, it need not be a quadratic polynomial.
The given linear polynomial y = f(x) has