Advertisements
Advertisements
प्रश्न
Find the weight of a lead pipe 35 cm long. The external diameter of the pipe is 2.4 cm and the thickness of the pipe is 2mm, given 1 cm3 of lead weighs 10 gm.
उत्तर
External radius 'R' = 1.2 cm
Internal radius 'r' = 1.0 cm ...(Since internal radius = external radius - thickness)
Height 'h' = 35 cm
∴ Volume of the pipe = πh[ R2 - r2 ]
= `22/7` x 35 x [(1.2)2 - (1.0)2]
= 48.4 cm3
∴ Weight of lead pie = 10 x 48.4 = 484 gm.
APPEARS IN
संबंधित प्रश्न
A soft drink is available in two packs − (i) a tin can with a rectangular base of length 5 cm and width 4 cm, having a height of 15 cm and (ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm. Which container has greater capacity and by how much?
`["Assume "pi=22/7]`
Given a cylindrical tank, in which situation will you find surface area and in which situation volume.
- To find how much it can hold
- Number of cement bags required to plaster it
- To find the number of smaller tanks that can be filled with water from it.
A cylinderical container with a diameter of base 42 cm contains sufficient water to submerge a rectangular solid of iron with dimesions 22 cm × 14 cm × 10.5 cm. Find the rise in level of the water when the solid is submerged.
Find the volume of the cylinder if the height (h) and radius of the base (r) are as given below.
r = 10.5 cm, h = 8 cm
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m. Calculate: the total area of the internal surface, excluding the base.
A glass cylinder with a diameter 20 cm has water to a height of 9 cm. A metal cube of 8 cm edge is immersed in it completely. Calculate the height by which the water will up in the cylinder. Answer correct of the nearest mm. (Take π = 3.142)
The volume of a cylinder which exactly fits in a cube of side a is ______.
Radius of a cylinder is r and the height is h. Find the change in the volume if the height is doubled.
Metallic discs of radius 0.75 cm and thickness 0.2 cm are melted to obtain 508.68 cm3 of metal. Find the number of discs melted (use π = 3.14).
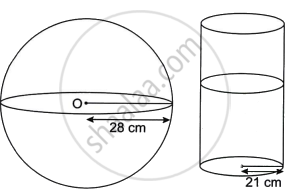
Oil is stored in a spherical vessel occupying `3/4` of its full capacity. Radius of this spherical vessel is 28 cm. This oil is then poured into a cylindrical vessel with a radius of 21 cm. Find the height of the oil in the cylindrical vessel (correct to the nearest cm). Take π = `22/7`