Advertisements
Advertisements
प्रश्न
Metallic discs of radius 0.75 cm and thickness 0.2 cm are melted to obtain 508.68 cm3 of metal. Find the number of discs melted (use π = 3.14).
उत्तर
Radius of metallic disc = 0.75 cm
Thickness of disc = 0.2 cm
Total volume of material which will be used in forming/melting of disc = 508.68 cm3
∴ Material required for one disc = Volume of cylinder
= πr2h
= `22/7 xx 0.75 xx 0.75 xx 0.2` ...[∵ Shape of a disc is a cylinder]
= 3.14 × 0.75 × 0.75 × 0.2
= 0.35325 cm3
Number of disc can be melted
= `"Total volume of metal obtained after melting"/"Volume of one disc"`
= `508.68/0.35325`
= 1440 discs
APPEARS IN
संबंधित प्रश्न
Diameter of cylinder A is 7 cm, and the height is 14 cm. Diameter of cylinder B is 14 cm and height is 7 cm. Without doing any calculations can you suggest whose volume is greater? Verify it by finding the volume of both the cylinders. Check whether the cylinder with greater volume also has greater surface area?

A cylindrical water tank of diameter 2.8 m and height 4.2 m is being fed by a pipe of diameter 7 cm through which water flows at the rate of 4 m s–1. Calculate, in minutes, the time it takes to fill the tank.
A solid metallic sphere of radius 6 cm is melted and made into a solid cylinder of height 32 cm. Find the:
(i) radius of the cylinder
(ii) curved surface area of the cylinder
Take π = 3.1
Find the volume of the cylinder if the circumference of the cylinder is 132 cm and height is 25 cm.
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m. Calculate: the total area of the internal surface, excluding the base.
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m. Calculate: the internal volume of the container in m3.
If the radius of a cylinder is doubled and height is halved, the volume will be doubled.
Two cylinders A and B are formed by folding a rectangular sheet of dimensions 20 cm × 10 cm along its length and also along its breadth respectively. Then volume of A is ______ of volume of B.
The thickness of a hollow metallic cylinder is 2 cm. It is 70 cm long with outer radius of 14 cm. Find the volume of the metal used in making the cylinder, assuming that it is open at both the ends. Also find its weight if the metal weighs 8 g per cm3.
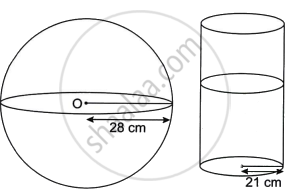
Oil is stored in a spherical vessel occupying `3/4` of its full capacity. Radius of this spherical vessel is 28 cm. This oil is then poured into a cylindrical vessel with a radius of 21 cm. Find the height of the oil in the cylindrical vessel (correct to the nearest cm). Take π = `22/7`