Advertisements
Advertisements
Question
Metallic discs of radius 0.75 cm and thickness 0.2 cm are melted to obtain 508.68 cm3 of metal. Find the number of discs melted (use π = 3.14).
Solution
Radius of metallic disc = 0.75 cm
Thickness of disc = 0.2 cm
Total volume of material which will be used in forming/melting of disc = 508.68 cm3
∴ Material required for one disc = Volume of cylinder
= πr2h
= `22/7 xx 0.75 xx 0.75 xx 0.2` ...[∵ Shape of a disc is a cylinder]
= 3.14 × 0.75 × 0.75 × 0.2
= 0.35325 cm3
Number of disc can be melted
= `"Total volume of metal obtained after melting"/"Volume of one disc"`
= `508.68/0.35325`
= 1440 discs
APPEARS IN
RELATED QUESTIONS
A lead pencil consists of a cylinder of wood with solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of the pencil is 14 cm, find the volume of the wood and that of the graphite.
`["Assume "pi=22/7]`
From a solid cylinder whose height is 16 cm and radius is 12 cm, a conical cavity of height 8 cm and of base radius 6 cm is hollowed out. Find the volume and total surface area of the remaining solid.
A circus tent is cylindrical to a height of 8 m surmounted by a conical part. If total height of the tent is 13 m and the diameter of its base is 24 m; calculate :
- total surface area of the tent,
- area of canvas, required to make this tent allowing 10% of the canvas used for folds and stitching.
Find the volume of the cylinder if the height (h) and radius of the base (r) are as given below.
r = 10.5 cm, h = 8 cm
A cylindrical vessel of height 24 cm and diameter 40 cm is full of water. Find the exact number of small cylindrical bottles, each of height 10 cm and diameter 8 cm, which can be filled with this water.
If the radius of a cylinder is doubled and height is halved, the volume will be doubled.
The radius and height of a cylinder are in the ratio 3 : 2 and its volume is 19,404 cm3. Find its radius and height.
A hollow garden roller of 42 cm diameter and length 152 cm is made of cast iron 2 cm thick. Find the volume of iron used in the roller.
Volume of a cylinder is 330 cm3. The volume of the cone having same radius and height as that of the given cylinder is:
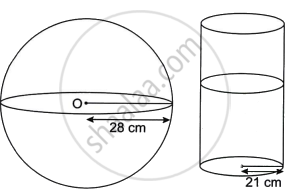
Oil is stored in a spherical vessel occupying `3/4` of its full capacity. Radius of this spherical vessel is 28 cm. This oil is then poured into a cylindrical vessel with a radius of 21 cm. Find the height of the oil in the cylindrical vessel (correct to the nearest cm). Take π = `22/7`