Advertisements
Advertisements
प्रश्न
Two cylinders A and B are formed by folding a rectangular sheet of dimensions 20 cm × 10 cm along its length and also along its breadth respectively. Then volume of A is ______ of volume of B.
उत्तर
Two cylinders A and B are formed by folding a rectangular sheet of dimensions 20 cm × 10 cm along its length and also along its breadth respectively. Then volume of A is twice of volume of B
Explanation:
We have, a rectangular sheet of dimensions 20 cm × 10 cm.
If we fold it along its length, which is 20 cm, then the resultant figure is a cylinder with height, h = 10 cm and base circumference, 2πr = 20 cm
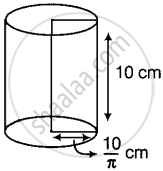
⇒ `r = 20/(2pi) = 10/pi cm`
∴ The volume of the cylinder, so formed = πr2h
= `pi xx 10/pi xx 10/pi xx 10`
= `1000/pi cm^3`
= V1 (say) ...(i)
Again, if we fold the rectangular sheet along its breadth, which is 10 cm, the figure so obtained is a cylinder with height h = 20 cm and the base circumference 2πr = 10 cm
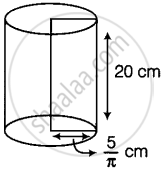
⇒ `r = 10/(2pi) = 5/pi cm`
∴ Volume of the cylinder = πr2h
= `pi xx 5/pi xx 5/pi xx 20`
= `500/pi cm^3`
= V2 (say) ...(ii)
i.e. V2 = 2V1
From equations, (i) and (ii), we see that the volume of A is twice the volume of B.
APPEARS IN
संबंधित प्रश्न
A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients?
`["Assume "pi=22/7]`
Given a cylindrical tank, in which situation will you find surface area and in which situation volume.
- To find how much it can hold
- Number of cement bags required to plaster it
- To find the number of smaller tanks that can be filled with water from it.
A cylindrical can, whose base is horizontal and of radius 3.5 cm, contains sufficient water so that when a sphere is placed in the can, the water just covers the sphere. Given that the sphere just fits into the can, calculate:
- the total surface area of the can in contact with water when the sphere is in it;
- the depth of water in the can before the sphere was put into the can.
How many cubic meters of earth must be dug out to make a well 28 m deep and 2.8 m in diameter ? Also, find the cost of plastering its inner surface at Rs 4.50 per sq meter.
A cylinder has a diameter of 20 cm. The area of the curved surface is 100 cm2 (sq. cm). Find the height of the cylinder correct to one decimal place.
The height and the radius of the base of a cylinder are in the ratio 3 : 1. If it volume is 1029 π cm3; find it total surface area.
3080 cm3 of water is required to fill a cylindrical vessel completely and 2310 cm3 of water is required to fill it upto 5 cm below the top. Find :
- radius of the vessel.
- height of the vessel.
- wetted surface area of the vessel when it is half-filled with water.
Two-cylinder have bases of the same size. The diameter of each is 14 cm. One of the cones is 10 cm high and the other is 20 cm high. Find the ratio between their volumes.
A conical container is fully filled with petrol. The radius is 10 m and the height is 15 m. If the container can release the petrol through its bottom at the rate of 25 cu. meter per minute, in how many minutes the container will be emptied. Round off your answer to the nearest minute.
From a pipe of inner radius 0.75 cm, water flows at the rate of 7 m per second. Find the volume in litres of water delivered by the pipe in 1 hour.
