Advertisements
Advertisements
प्रश्न
Diameter of cylinder A is 7 cm, and the height is 14 cm. Diameter of cylinder B is 14 cm and height is 7 cm. Without doing any calculations can you suggest whose volume is greater? Verify it by finding the volume of both the cylinders. Check whether the cylinder with greater volume also has greater surface area?

उत्तर
The heights and diameters of these cylinders A and B are interchanged.
We know that,
Volume of cylinder = πr2h
If measures of r and h are same, then the cylinder with greater radius will have greater area
Radius of cylinder A = `7/2` cm
Radius of cylinder B = `(14/2)` cm = 7 cm
As the radius of cylinder B is greater, therefore, the volume of cylinder B will be greater.
Let us verify it by calculating the volume of both the cylinders.
Volume of cylinder A = πr2h
= `(22/7 xx 7/2 xx 7/2 xx 14) cm^3`
= 539 cm3
Volume of cylinder B = πr2h
= `(22/7 xx 7 xx 7 xx 7)` cm3
= 1078 cm3
The volume of cylinder B is greater.
Surface area of cylinder A = 2πr (r + h)
= `[2 xx 22/7 xx 7/2 (7/2 + 14)] cm^2`
= `[22 xx ((7+28)/2)] cm^2`
= `(22 xx 35/2) cm^2`
= 385 cm2
Surface area of cylinder B = 2πr (r + h)
= `[2 xx22/7 xx 7 xx (7 + 7)]` cm2
= (44 × 14) cm2
= 616 cm2
Thus, the surface area of cylinder B is also greater than the surface area of cylinder A.
APPEARS IN
संबंधित प्रश्न
The capacity of a closed cylindrical vessel of height 1 m is 15.4 litres. How many square metres of metal sheet would be needed to make it?
`["Assume "pi=22/7]`
A hemispherical bowl of internal radius 9 cm is full of liquid. This liquid is to be filled into conical shaped small container each of diameter 3 cm and height 4 cm. How many container are necessary to empty the bowl?
A vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylindrical part is `4 2/3` m and the diameter of hemisphere is 3.5 m. Calculate the capacity and the internal surface area of the vessel.
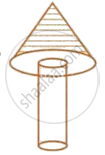
A wooden toy is in the shape of a cone mounted on a cylinder as shown alongside. If the height of the cone is 24 cm, the total height of the toy is 60 cm and the radius of the base of the cone = twice the radius of the base of the cylinder = 10 cm; find the total surface area of the toy. [Take π = 3.14]
The total surface area of a hollow cylinder, which is open from both the sides, is 3575 cm2; area of its base ring is 357.5 cm2 and its height is 14 cm. Find the thickness of the cylinder.
A closed cylindrical tank, made of thin ironsheet, has diameter = 8.4 m and height 5.4 m. How much metal sheet, to the nearest m2, is used in making this tank, if `1/15` of the sheet actually used was wasted in making the tank?
Two-cylinder have bases of the same size. The diameter of each is 14 cm. One of the cones is 10 cm high and the other is 20 cm high. Find the ratio between their volumes.
A glass cylinder with a diameter 20 cm has water to a height of 9 cm. A metal cube of 8 cm edge is immersed in it completely. Calculate the height by which the water will up in the cylinder. Answer correct of the nearest mm. (Take π = 3.142)
The volume of a cylinder whose radius r is equal to its height is ______.
The ratio of radii of two cylinders is 1 : 2 and heights are in the ratio 2 : 3. The ratio of their volumes is ______.
