Question

For a series LCR circuit, I vs ω curve is shown:

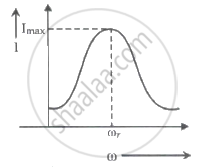
1. To the left of ω_r, the circuit is mainly capacitive.
2. To the left of ω_r, the circuit is mainly inductive.
3. At ω_r, impedance of the circuit is equal to the resistance of the circuit.
4.  At ω_r, impedance of the circuit is 0.

विकल्प

• (a) and (d) only 

• (b) and (d) only 

• (a) and (c) only

• (b) and (c) only

Answer 1

At ω_r, impedance of the circuit is equal to the resistance of the circuit.

Explanation:

At resonance X_L = X_C and impedance of circuit is minimum and is equal to R and current is maximum.

At resonance, ω₀ = `1/sqrt("LC")`

⇒ When current exceeds voltage and the circuit is capacitive, the potential drop across the capacitor exceeds that across the inductor.

⇒ The circuit becomes inductive if the potential drop across the inductor is greater than the potential drop across the capacitor.

Thus, i₀X_L > i₀X_C Circuit is inductive

X_L > X_C

ωL > `1/(ω"C")`

ω² > `1/sqrt("LC")`

ω > `sqrt(1/sqrt("LC"))`

ω > ω_R

i₀X_C > i₀X_L Circuit is inductive

X_C > X_L

1/ωC  > ωL

ω < `1/sqrt("LC")`

ω < `sqrt(1/sqrt("LC"))`

ω < ω_R