Advertisements
Advertisements
प्रश्न
For each of the following statements state whether true(T) or false (F)
The sum of the squares on the sides of a rhombus is equal to the sum of the squares on its diagonals.
उत्तर
True
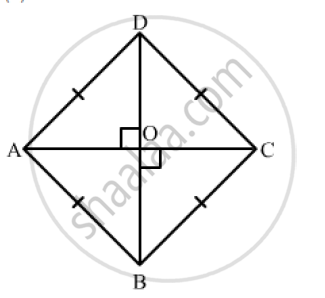
Suppose ABCD is a rhombus having AC and BD its diagonals.
Since, the diagonals of a rhombus perpendicular bisect each other.
Hence, AOC is a right angle triangle
In right triangle AOC
By using Pythagoras theorem, we have
`AB^2=((AC)/2)^2+((BD)/2)^2`
[∴ Diagonals of a rhombus perpendicularly bisect each other]
⇒ `AB^2=((AC)/2)^2+((BD)/2)^2`
⇒ `4AB^2=AC^2+BD^2`
⇒ `AB^2+AB^2+AB^2+AB^2=AC^2+BD^2`
⇒ `AB^2+BC^2+CD^2+DA^2=AC^2+BD^2` [∵𝐴𝑙𝑙 𝑠𝑖𝑑𝑒𝑠 𝑜𝑓 𝑎 𝑟ℎ𝑜𝑚𝑏𝑢𝑠 𝑎𝑟𝑒 𝑒𝑞𝑢𝑎𝑙]
APPEARS IN
संबंधित प्रश्न
All ______ triangles are similar.
Two polygons of the same number of sides are similar, if (a) their corresponding angles are ______ and (b) their corresponding sides are ______. (equal, proportional)
Write the truth value (T/F) of each of the following statement
Two polygons are similar, if their corresponding sides are proportional.
Write the truth value (T/F) of each of the following statement
Two polygons are similar if their corresponding angles are proportional.
Write the truth value (T/F) of each of the following statement
Two triangles are similar if their corresponding angles are proportional.
For each of the following statements state whether true(T) or false (F)
Two circles with different radii are similar.
If O is Any Point Inside a Rectangle Abcd Then `Oa^2+Oc^2=Ob^2+Od^2`
ΔPQR is an equilateral triangle with each side of length 2p. If PS ⊥ QR, then PS is equal to ______.
In a rhombus if d1 = 16 cm, d2 = 12 cm, then the length of the side of the rhombus is ______.
Observe the figures given below carefully and answer the questions:
| Figure A | 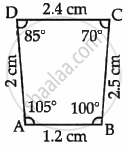 |
 |
| Figure B |  |
 |
| Figure C | 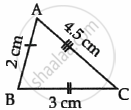 |
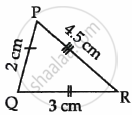 |
- Name the figure(s) where in two figures are similar.
- Name the figure(s) where in the figures are congruent.
-
- Prove that congruent triangles are also similar but not the converse.
OR - What more is least needed for two similar triangles to be congruent?
- Prove that congruent triangles are also similar but not the converse.
