Advertisements
Advertisements
प्रश्न
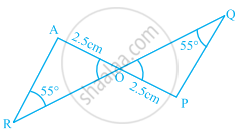
For the given pair of triangles state the criterion that can be used to determine the congruency?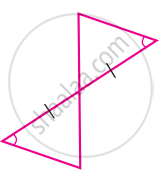
उत्तर
One of the sides and one of the angles are equal.
∴ One more angle is vertically opposite angle and so it is also equal.
ASA criterion is used.
APPEARS IN
संबंधित प्रश्न
By applying the ASA congruence rule, it is to be established that ∆ABC ≅ ∆QRP and it is given that BC = RP. What additional information is needed to establish the congruence?
In Fig, can you use the ASA congruence rule and conclude that ∆AOC ≅ ∆BOD?

In the given figure, AC ≡ AD and ∠CBD ≡ ∠DEC. Prove that ∆BCF ≡ ∆EDF.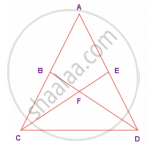
In the given figure, Δ______ ≅ ΔPQR.
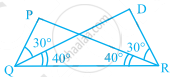
In the given figure, ∆ARO ≅ ∆______.
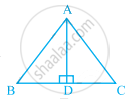
In the given figure, AD ⊥ BC and AD is the bisector of angle BAC. Then, ∆ABD ≅ ∆ACD by RHS.
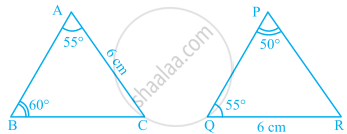
In the given pairs of triangles of figure, applying only ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
In the given pairs of triangles of figure, applying only ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
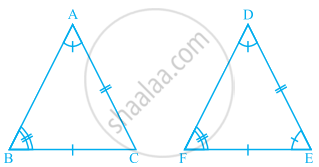
In the given pairs of triangles of figure, applying only ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
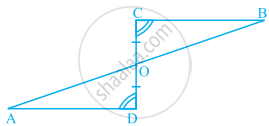
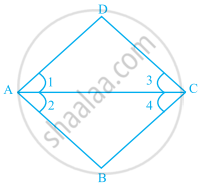
In the given figure, ∠1 = ∠2 and ∠3 = ∠4.
- Is ∆ADC ≅ ∆ABC? Why ?
- Show that AD = AB and CD = CB.