Advertisements
Advertisements
Question
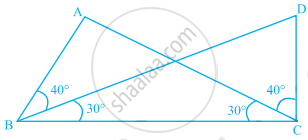
For the given pair of triangles state the criterion that can be used to determine the congruency?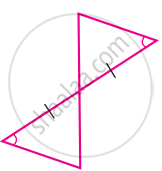
Solution
One of the sides and one of the angles are equal.
∴ One more angle is vertically opposite angle and so it is also equal.
ASA criterion is used.
APPEARS IN
RELATED QUESTIONS
Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by the ASA congruence rule. In the case of congruence, write it in symbolic form.
∆DEF, ∠D = 60º, ∠F = 80º, DF = 6 cm.
∆PQR, ∠Q = 60º, ∠R = 80º, QP = 6 cm.
In the given figure, AC ≡ AD and ∠CBD ≡ ∠DEC. Prove that ∆BCF ≡ ∆EDF.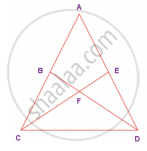
State whether the two triangles are congruent or not. Justify your answer
For the given pair of triangles state the criterion that can be used to determine the congruency?
In the given figure, AD = CD and AB = CB. Identify the other three pairs that are equal
In the given figure, AD ⊥ BC and AD is the bisector of angle BAC. Then, ∆ABD ≅ ∆ACD by RHS.
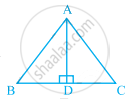
In the given pairs of triangles of figure, applying only ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
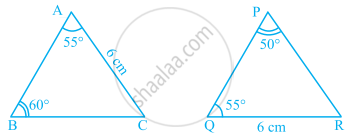
In the given pairs of triangles of figure, applying only ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
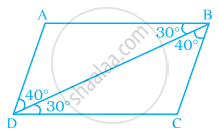
In the given pairs of triangles of figure, applying only ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
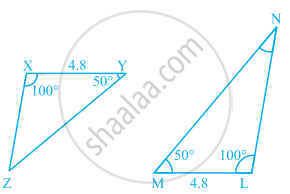
Observe the given figure and state the three pairs of equal parts in triangles ABC and DBC.
- Is ∆ABC ≅ ∆DCB? Why?
- Is AB = DC? Why?
- Is AC = DB? Why?