Advertisements
Advertisements
प्रश्न
From the adjacent figure:
(i) Write the coordinates of the points A, B, and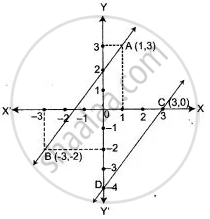
(ii) Write the slope of the line AB.
(iii) Line through C, drawn parallel to AB, intersects Y-axis at D. Calculate the co-ordinates of D.
उत्तर
(i) Coordinates of the points A, B and C are (1, 3), (-3, -2) and (3, 0) respectively.
(ii) Slope of AB = `(-2 - 3)/(-3 - 1) = (5)/(4)`.
(iii) Line through C(3, 0) and parallel to AB.
∴ Slope = `(5)/(4)`.
∴ Equation to the line is
y - y1 = m(x - x1)
y - 0 = `(5)/(4)(x - 3)`
4y = 5x - 15
This line intersects Y-axis at D.
∴ On solving
4y = 5x - 15
and x = 0, ...(Equation to Y-axis)
We get, 4y = -15
y = `-(15)/(4)`
∴ Coordinates of point D are `(0, -15/7)`.
APPEARS IN
संबंधित प्रश्न
Calculate the co-ordinates of the point P which divides the line segment joining: A (–4, 6) and B (3, –5) in the ratio 3 : 2
In what ratio does the point (1, a) divide the join of (–1, 4) and (4, –1)? Also, find the value of a.
Calculate the ratio in which the line joining A(-4,2) and B(3,6) is divided by point p(x,3). Also, find x
Find the image of the point A(5,3) under reflection in the point P(-1,3).
Prove that the points A(-5, 4), B(-1, -2) and C(S, 2) are the vertices of an isosceles right-angled triangle. Find the coordinates of D so that ABCD is a square.
Show that the points A(1, 3), B(2, 6), C(5, 7) and D(4, 4) are the vertices of a rhombus.
= `a(1/t^2 + 1) = (a(t^2 + 1))/t^2`
Now `(1)/"SP" + (1)/"SQ" = (1)/(a(t^2 + 1)) + (1 xx t^2)/(a(t^2 + 1)`
= `((1 + t^2))/(a(t^2 + 1)`
`(1)/"SP" + (1)/"SQ" = (1)/a`.
If the line joining the points A(4, - 5) and B(4, 5) is divided by the point P such that `"AP"/"AB" = (2)/(5)`, find the coordinates of P.
The midpoint of the line segment AB shown in the diagram is (4, – 3). Write down the coordinates of A and B.
In the following figure line APB meets the X-axis at A, Y-axis at B. P is the point (4, -2) and AP: PB = 1: 2. Write down the coordinates of A and B.
Determine the centre of the circle on which the points (1, 7), (7 – 1), and (8, 6) lie. What is the radius of the circle?
