Advertisements
Advertisements
प्रश्न
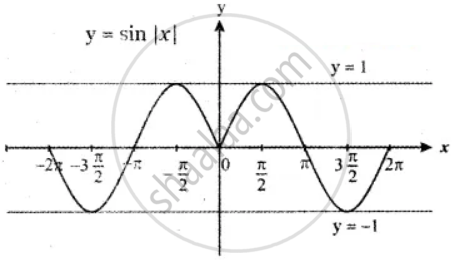
From the curve y = sin x, draw y = sin |x| (Hint: sin(−x) = − sin x)
उत्तर
y = sin |x|
(a) Consider y = sin x
| x | 0 | `pi/2` | π | `3 pi/2` | 2π | `- pi/2` | – π | `- 3 pi/2` | – 2π |
| y | 0 | 1 | 0 | – 1 | 0 | – 1 | 0 | 1 | 0 |

(b) Consider y = sin |x|
y = `{{:(sin x, "if" x ≥ 0),(sin (- x) = - sin x, "if" x < 0):}`
y = `{{:(sin x, "if" x ≥ 0),(- sin x, "if" x < 0):}`
x = 0 ⇒ y = sin x ⇒ y = sin 0 = 0
x = `pi/2` ⇒ y = sin x ⇒ y = `sin pi/2` = 0
x = π ⇒ y = sin x ⇒ y = sin π = 0
x = `3 pi/2` ⇒ y = sin x ⇒ y = `sin 3 pi/2`
⇒ y = `sin (pi + pi/2) = - sin pi/2` = – 1
x = 2π ⇒ y = sin x ⇒ y = sin 2π = 0
x =`- pi/2` ⇒ y = – sin x ⇒ y = `- sin (- pi/2)`
⇒ y = `sin pi/2` = 1
x = – π ⇒ y = – sin x ⇒ y = – sin (– π)
⇒ y = sin π = 0
x = `- 3 pi/2` ⇒ y = – sin x ⇒ y = `- sin (- 3 pi/2)`
⇒ y = `sin (3pi)/2`
⇒ y = `sin(pi + pi/2)`
⇒ y = `- sin pi/2` = – 1
x = – 2π ⇒ y = – sin x ⇒ y = – sin (– 2π)
⇒ y = sin 2π = 0
| x | 0 | `pi/2` | π | `3 pi/2` | 2π | `- pi/2` | – π | `- 3 pi/2` | – 2π |
| y | 0 | 1 | 0 | – 1 | 0 | 1 | 0 | – 1 | 0 |
APPEARS IN
संबंधित प्रश्न
For the curve y = x3 given in Figure 1.67, draw
y = −x3 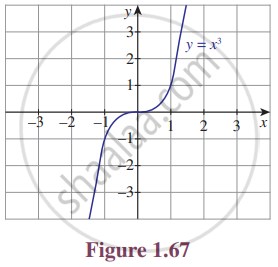
For the curve y = x3 given in Figure 1.67, draw
y = x3 − 1 
For the curve y = x3 given in Figure 1.67, draw
y = (x + 1)3 with the same scale
For the curve y = `x^((1/3))` given in Figure 1.68, draw
y = `- x^((1/3))`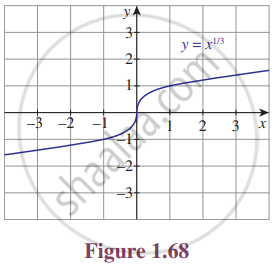
For the curve y = `x^((1/3))` given in Figure 1.68, draw
y = `x^((1/3)) + 1`
For the curve y = `x^((1/3))` given in Figure 1.68, draw
y = `(x + 1)^((1/3))`
Write the steps to obtain the graph of the function y = 3(x − 1)2 + 5 from the graph y = x2
From the curve y = sin x, graph the function.
y = sin(− x)
From the curve y = sin x, graph the function
y = − sin(−x)
From the curve y = sin x, graph the function
y = `sin(pi/2 + x)` which is cos x
From the curve y = x, draw y = x + 1
From the curve y = x, draw y = `1/2 x + 1`
From the curve y = x, draw 2x + y + 3 = 0
From the curve y = |x|, draw y = |x − 1| + 1
From the curve y = |x|, draw y = |x + 1| − 1
