Advertisements
Advertisements
प्रश्न
Given:
A = {Natural numbers less than 10}
B = {Letters of the word ‘PUPPET’}
C = {Squares of first four whole numbers}
D = {Odd numbers divisible by 2}.
Find: n(A ∪ D)
उत्तर
Here,
A= {1, 2, 3, 4, 5, 6, 7, 8, 9}
B = {P, U, E, T}
C = {0, 1, 4, 9}
D = { } or Φ
A ∪ D = {1, 2, 3, 4, 5, 6, 7, 8, 9}
n(A ∪ D) = 9
APPEARS IN
संबंधित प्रश्न
Write the cardinal number of the following set:
A = {0, 1, 2, 4}
Given:
A = {Natural numbers less than 10}
B = {Letters of the word ‘PUPPET’}
C = {Squares of first four whole numbers}
D = {Odd numbers divisible by 2}.
Find: n(D)
Given:
A = {Natural numbers less than 10}
B = {Letters of the word ‘PUPPET’}
C = {Squares of first four whole numbers}
D = {Odd numbers divisible by 2}.
Find: n(B ∪ D)
Given:
A = {Natural numbers less than 10}
B = {Letters of the word ‘PUPPET’}
C = {Squares of first four whole numbers}
D = {Odd numbers divisible by 2}.
Find: n(C ∩ D)
State true or false for the following. Correct the wrong statement.
If B = {1, 5, 51, 15, 5, 1}, then n(B) = 6.
State true or false for the following. Correct the wrong statement.
If T ={a, l, a, h, b, d, h), then n(T) = 5
Each student in a class of 35 plays atleast one game among chess, carrom and table tennis. 22 play chess, 21 play carrom, 15 play table tennis, 10 play chess and table tennis, 8 play carrom and table tennis and 6 play all the three games. Find the number of students who play only carrom (Hint: Use Venn diagram)
If n(A ∪ B ∪ C) = 100, n(A) = 4x, n(B) = 6x, n(C) = 5x, n(A ∩ B) = 20, n(B ∩ C) = 15, n(A ∩ C) = 25 and n(A ∩ B ∩ C) = 10, then the value of x is
The shaded region in the Venn diagram is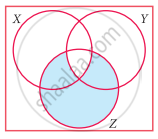
In a city, 40% people like only one fruit, 35% people like only two fruits, 20% people like all the three fruits. How many percentage of people do not like any one of the above three fruits?
