Advertisements
Advertisements
प्रश्न
Given `overline"AB"` of length 7.3 cm and `overline"CD"` of length 3.4 cm, construct a line segment `overline"XY"` such that the length of `overline"XY"` is equal to the difference between the lengths of `overline"AB"` and `overline"CD"`. Verify by measurement.
उत्तर
- Given that, `overline"AB"` = 7.3 cm and `overline"CD"` = 3.4 cm


- Adjust the compasses up to the length of CD and put the pointer of the compasses at A. Draw an arc to cut AB at P.
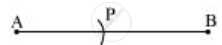
- Adjust the compasses up to the length of PB. Now draw a line l and mark a point X on it.

- Now, putting the pointer of compasses at point X, draw an arc to cut the line at Y.

`overline"XY"` is the required line segment.
APPEARS IN
संबंधित प्रश्न
Draw any circle and mark points A, B and C such that
- A is on the circle.
-
B is in the interior of the circle.
- C is in the exterior of the circle.
Draw a line segment of length 7.3 cm using a ruler.
Construct a line segment of length 5.6 cm using ruler and compasses.
Construct `overline"AB"` of length 7.8 cm. From this, cut off `overline"AC"` of length 4.7 cm. Measure `overline"BC"`.
Given `overline"AB"` of length 3.9 cm, construct `overline"PQ"` such that the length of `overline"PQ"` is twice that of `overline"AB"`. Verify by measurement.

(Hint: construct `overline"PX"` such that length of `overline"PX"` = length of `overline"AB"`; then cut off `overline"XQ"` such that `overline"XQ"` also has the length of `overline"AB"`.)
