Question

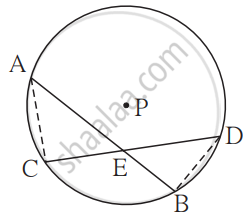
Given:

Chords AB and CD of a circle with centre P intersect at point E.

To prove:

AE × EB = CE × ED

Construction:

Draw seg AC and seg BD.

Fill in the blanks and complete the proof.

Proof:

In Δ CAE and Δ BDE,

∠AEC ≅ ∠DEB    ...`square`

`square` ≅ ∠BDE    ...(angles inscribed in the same arc)

∴ ΔCAE ~ ΔBDE    ...`square`

∴ `square/ ("DE") = ("CE")/square`    ...`square` 

∴ AE × EB = CE × ED.

Answer 1

Given that chords AB and CD of a circle intersect at point E, we need to prove:

AE × EB = CE × ED

In △CAE and △BDE:

1. ∠AEC ≅ ∠DEB → Vertically opposite angles.
2. ∠CAE ≅ ∠BDE → Angles inscribed in the same arc.

△CAE ∼ △BDE

Thus, corresponding sides are proportional:

`(AE)/(DE) = (CE)/(EB)`

Cross multiplying:

AE × EB = CE × ED

1. ∠AEC ≅ ∠DEB → Vertically opposite angles.
2. ∠CAE ≅ ∠BDE → Angles inscribed in the same arc.
3. △CAE ∼ △BDE → By AA similarity.
4. `(AE)/(DE) = (CE)/(EB)` → By property of similar triangles.
5. AE × EB = CE × ED → By cross multiplication.