Advertisements
Advertisements
प्रश्न
I धारावाही, N फेरों और R त्रिज्या वाली वृत्ताकार कुंडली के लिए, इसके अक्ष पर, केन्द्र से x दूरी पर स्थित किसी बिन्दु पर चुम्बकीय क्षेत्र के लिए निम्नलिखित व्यंजक है-
B =
(a) स्पष्ट कीजिए, इससे कुंडली के केन्द्र पर चुम्बकीय क्षेत्र के लिए सुपरिचित परिणाम कैसे प्राप्त किया जा सकता है?
(b) बराबर त्रिज्या R एवं फेरों की संख्या N, वाली दो वृत्ताकार कुंडलियाँ एक-दूसरे से R दूरी पर एक-दूसरे के समान्तर, अक्ष मिलाकर रखी गई हैं। दोनों में समान विद्युत धारा एक ही दिशा में प्रवाहित हो रही है। दर्शाइए कि कुण्डलियों के अक्ष के लगभग मध्यबिन्दु पर क्षेत्र, एक बहुत छोटी दूरी के लिए जो कि Rसे कम है, एकसमान है और इस क्षेत्र का लगभग मान निम्नलिखित है-
B =
[बहुत छोटे से क्षेत्र पर एकसमान चुम्बकीय क्षेत्र उत्पन्न करने के लिए बनायी गई ऊपर वर्णित व्यवस्था हेल्महोल्ट्ज कुण्डलियों के नाम से जानी जाती है।]
उत्तर
(a) दिए गए सूत्र में x = 0 रखने पर,
B =
जो की स्पष्टता कुंडली के केन्द्र पर चुम्बकीय क्षेत्र का सूत्र है।
अतः दिए गए सूत्र से कुंडली के केन्द्र पर चुम्बकीय क्षेत्र ज्ञात करने के लिए x के स्थान पर शून्य रखना होगा।
(b) माना इस प्रकार की दो कुंडलियों के केन्द्रों को मिलाने वाली रेखा C1C2 का मध्य बिन्दु C है तथा इससे d दूरी (दूरी d बहुत छोटी है) पर एक बिन्दु P स्थित है।
तब प्रथम कुंडली के लिए,
तब दूसरी कुंडली के लिए
∵ दोनों कुंडली पूर्णतः एक जैसी हैं तथा दोनों में धाराएँ भी एक ही दिशा में हैं;
अतः बिन्दु P पर दोनों के कारण चुम्बकीय क्षेत्र एक ही दिशा में होंगे।
∵ बिन्दु P पर नैट चुम्बकीय क्षेत्र
B =
APPEARS IN
संबंधित प्रश्न
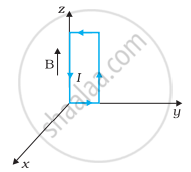
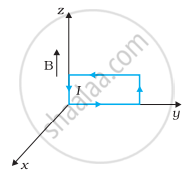
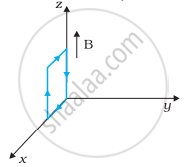
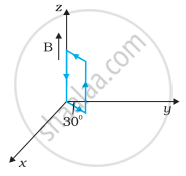
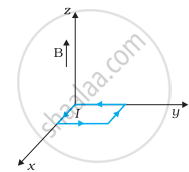
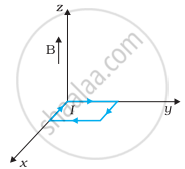
धनात्मक z-दिशा में 3000 G की एक एकसमान चुम्बकीय क्षेत्र लगाया गया है। एक आयताकार लूप जिसकी भुजाएँ 10 cm एवं 5 cm और जिसमें 12 A धारा प्रवाहित हो रही है, इस क्षेत्र में रखा है। चित्र 4.7 में दिखायी गई लूप की विभिन्न स्थितियों में इस पर लगने वाला बल-युग्म आघूर्ण क्या है? हर स्थिति में बल क्या है? स्थायी सन्तुलन वाली स्थिति कौन-सी है?
 |
 |
 |
| (a) | (b) | (c) |
 |
 |
 |
| (d) | (e) | (f) |
