Advertisements
Advertisements
प्रश्न
If A = [1, 2, 3], B = [4, 5, 6], which of the following are relations from A to B? Give reasons in support of your answer.
(i) [(1, 6), (3, 4), (5, 2)]
(ii) [(1, 5), (2, 6), (3, 4), (3, 6)]
(iii) [(4, 2), (4, 3), (5, 1)]
(iv) A × B.
उत्तर
Given:
A = {1, 2, 3} and B = {4, 5, 6}
Thus, we have:
A × B = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
(i) {(1, 6), (3, 4), (5, 2)}
Since it is not a subset of A × B, it is not a relation from A to B.
(ii) {(1, 5), (2, 6), (3, 4), (3, 6)}
Since it is a subset of A × B, it is a relation from A to B.
(iii) {(4, 2), (4, 3), (5, 1)}
Since it is not a subset of A × B, it is not a relation from A to B.
(iv) A × B
Since it is a subset (equal to) of A × B, it is a relation from A to B.
APPEARS IN
संबंधित प्रश्न
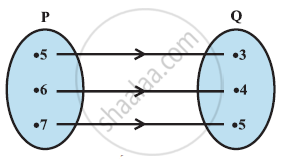
The given figure shows a relationship between the sets P and Q. Write this relation
- in set-builder form.
- in roster form.
What is its domain and range?
The relation f is defined by f(x) = `{(x^2,0<=x<=3),(3x,3<=x<=10):}`
The relation g is defined by g(x) = `{(x^2, 0 <= x <= 2),(3x,2<= x <= 10):}`
Show that f is a function and g is not a function.
Find the inverse relation R−1 in each of the cases:
(ii) R = {(x, y), : x, y ∈ N, x + 2y = 8}
Let A = [1, 2] and B = [3, 4]. Find the total number of relation from A into B.
Determine the domain and range of the relation R defined by
(i) R = [(x, x + 5): x ∈ (0, 1, 2, 3, 4, 5)]
Let R be a relation on N × N defined by
(a, b) R (c, d) ⇔ a + d = b + c for all (a, b), (c, d) ∈ N × N
Show that:
(ii) (a, b) R (c, d) ⇒ (c, d) R (a, b) for all (a, b), (c, d) ∈ N × N
Let A and B be two sets such that n(A) = 3 and n(B) = 2. If (x, 1), (y, 2), (z, 1) are in A × B, write A and B
Let A = [1, 2, 3, 5], B = [4, 6, 9] and R be a relation from A to B defined by R = {(x, y) : x − yis odd}. Write R in roster form.
If `(x + 1/3, y/3 - 1) = (1/2, 3/2)`, find x and y
Express {(x, y) / x2 + y2 = 100, where x, y ∈ W} as a set of ordered pairs
Write the relation in the Roster Form. State its domain and range
R2 = `{("a", 1/"a") // 0 < "a" ≤ 5, "a" ∈ "N"}`
Write the relation in the Roster Form. State its domain and range
R3 = {(x, y)/y = 3x, y∈ {3, 6, 9, 12}, x∈ {1, 2, 3}
Write the relation in the Roster Form. State its domain and range
R4 = {(x, y)/y > x + 1, x = 1, 2 and y = 2, 4, 6}
Write the relation in the Roster Form. State its domain and range
R5 = {(x, y)/x + y = 3, x, y∈ {0, 1, 2, 3}
Write the relation in the Roster Form. State its domain and range
R8 = {(a, b)/b = a + 2, a ∈ z, 0 < a < 5}
Select the correct answer from given alternative.
The relation ">" in the set of N (Natural number) is
Select the correct answer from given alternative
If A = {a, b, c} The total no. of distinct relations in A × A is
Answer the following:
Determine the domain and range of the following relation.
R = {(a, b)/a ∈ N, a < 5, b = 4}
Let A = {1, 2, 3, 4, …, 45} and R be the relation defined as “is square of ” on A. Write R as a subset of A × A. Also, find the domain and range of R
Represent the given relation by
(a) an arrow diagram
(b) a graph and
(c) a set in roster form, wherever possible
{(x, y) | y = x + 3, x, y are natural numbers < 10}
Multiple Choice Question :
If there are 1024 relation from a set A = {1, 2, 3, 4, 5} to a set B, then the number of elements in B is
Let X = {a, b, c, d} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it reflexive
Let X = {a, b, c, d} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it symmetric
Let A = {a, b, c} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it reflexive
Let A = {a, b, c} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it symmetric
On the set of natural numbers let R be the relation defined by aRb if 2a + 3b = 30. Write down the relation by listing all the pairs. Check whether it is transitive
Prove that the relation “friendship” is not an equivalence relation on the set of all people in Chennai
Find the domain and range of the relation R given by R = {(x, y) : y = `x + 6/x`; where x, y ∈ N and x < 6}.
If R1 = {(x, y) | y = 2x + 7, where x ∈ R and – 5 ≤ x ≤ 5} is a relation. Then find the domain and Range of R1.
Is the given relation a function? Give reasons for your answer.
f = {(x, x) | x is a real number}
Let f: R `rightarrow` R be defined by f(x) = `x/(1 + x^2), x ∈ R`. Then the range of f is ______.
Let S = {x ∈ R : x ≥ 0 and `2|sqrt(x) - 3| + sqrt(x)(sqrt(x) - 6) + 6 = 0}`. Then S ______.
A relation on the set A = {x : |x| < 3, x ∈ Z}, where Z is the set of integers is defined by R = {(x, y) : y = |x| ≠ –1}. Then the number of elements in the power set of R is ______.
Let A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} and f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}. Is the following true?
f is a function from A to B
Justify your answer in case.
