Advertisements
Advertisements
प्रश्न
If α, β are the zeros of polynomial f(x) = x2 − p (x + 1) − c, then (α + 1) (β + 1) =
विकल्प
c − 1
1 − c
c
1 + c
उत्तर
Since `alpha` and `beta` are the zeros of quadratic polynomial
f(x) = x2 − p (x + 1) − c
`= x^2 - px p -c`
`alpha + ß = - (text{coefficient of x})/(text{coefficient of } x^2)`
`=-((-p)/1)`
`= p`
`alpha xx ß = (\text{constat term})/(text{coefficient of} x^2)`
`= (-p-c)/1`
`= -p-c`
We have
`(alpha+1)(beta+1)`
`= alpha beta+ beta + alpha +1`
`= alphabeta + (alpha+beta)+1`
`= - p-c +(p)+1`
`- cancel(p)- c+ cancel(p) +1`
`= -c+1`
`= 1-c`
The value of `(alpha +1) (beta +1)` is ` 1- c`.
Hence, the correct choice is `(b)`
APPEARS IN
संबंधित प्रश्न
Define degree of a polynomial.
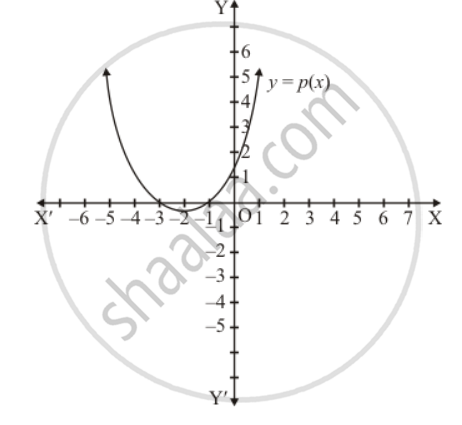
In Fig. 2.17, the graph of a polynomial p(x) is given. Find the zeros of the polynomial.
If zeros of the polynomial f(x) = x3 − 3px2 + qx − r are in A.P., then
Divide. Write the quotient and the remainder.
40m5 ÷ 30m3
Divide. Write the quotient and the remainder.
(6x5 − 4x4 + 8x3 + 2x2) ÷ 2x2
The below picture are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.




If α and `1/α` are the zeroes of the quadratic 2x2 − x + 8k, polynomial 2 then k is:
For the polynomial `((x^3 + 2x + 1))/5 - 7/2 x^2 - x^6`, write the coefficient of x3
For the polynomial `((x^3 + 2x + 1))/5 - 7/2 x^2 - x^6`, write the constant term
Classify the following as a constant, linear, quadratic and cubic polynomials:
3
Classify the following as a constant, linear, quadratic and cubic polynomials:
1 + x + x2
