Advertisements
Advertisements
प्रश्न
If α, β are the zeros of the polynomial f(x) = x2 + x + 1, then \[\frac{1}{\alpha} + \frac{1}{\beta} =\]
विकल्प
1
-1
0
None of these
उत्तर
Since `alpha` and ß are the zeros of the quadratic polynomial f(x) = x2 + x + 1,
`alpha + ß = - (text{coefficient of x})/(text{coefficient of } x^2)`
`= (-1)/1=1`
`alpha + ß = (\text{constat term})/(text{coefficient of} x^2)`
`= 1/1=1`
we have
`= 1/alpha+ 1/ ß`
` (ß +alpha)/(alpha ß)`
`=-1/1`
`=-1`
The value of `1/alpha + 1/ß ` is -1
Hence, the correct choice is (b).
APPEARS IN
संबंधित प्रश्न
Classify the following polynomials as polynomials in one-variable, two variables etc:
`x^2-2tx+7t^2-x+t`
For what value of k, is −3 a zero of the polynomial x2 + 11x + k?
If a quadratic polynomial f(x) is not factorizable into linear factors, then it has no real zero. (True/False)
If the graph of quadratic polynomial ax2 + bx + c cuts negative direction of y-axis, then what is the sign of c?
If Q.No. 14, c =
Identify the following expression is polynomial. If not give reason:
`sqrt(5)x^2 + sqrt(3)x + sqrt(2)`
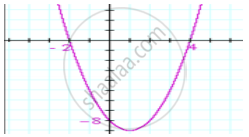
An asana is a body posture, originally and still a general term for a sitting meditation pose, and later extended in hatha yoga and modern yoga as exercise, to any type of pose or position, adding reclining, standing, inverted, twisting, and balancing poses. In the figure, one can observe that poses can be related to representation of quadratic polynomial.


In the graph, how many zeroes are there for the polynomial?
Degree of the polynomial 4x4 + 0x3 + 0x5 + 5x + 7 is ______.
Determine the degree of the following polynomial:
–10
Classify the following as a constant, linear, quadratic and cubic polynomials:
`5t - sqrt(7)`
