Advertisements
Advertisements
प्रश्न
If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD show that ar (EFGH) = 1/2ar (ABCD)
उत्तर
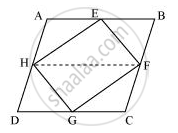
Let us join HF.
In parallelogram ABCD,
AD = BC and AD || BC (Opposite sides of a parallelogram are equal and parallel)
AB = CD (Opposite sides of a parallelogram are equal)
⇒ 1/2AD = 1/2BC and AH || BF
⇒ AH = BF and AH || BF (∵ H and F are the mid-points of AD and BC)
Therefore, ABFH is a parallelogram.
Since ΔHEF and parallelogram ABFH are on the same base HF and between the same parallel lines AB and HF,
∴ Area (ΔHEF) = 1/2Area (ABFH) ... (1)
Similarly, it can be proved that
Area (ΔHGF) = 1/2Area (HDCF) ... (2)
On adding equations (1) and (2), we obtain
Area(ΔHEF) + Area(ΔHGF) = 1/2Area (ABFH) + 1/2Area (HDCF)
= 1/2[Area (ABFH) + Area (HDCF)]
⇒ Area(EFGH) = 1/2Area(ABCD)
APPEARS IN
संबंधित प्रश्न
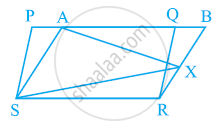
In the given figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = 1/2ar (PQRS)
Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
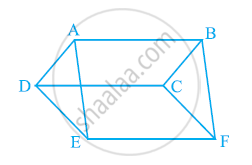
In the following figure, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).
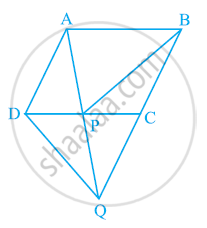
In the following figure, ABCD is parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that
ar (BPC) = ar (DPQ).
[Hint: Join AC.]
In the given below fig. ABCD, ABFE and CDEF are parallelograms. Prove that ar (ΔADE)
= ar (ΔBCF)
In which of the following figures, you find two polygons on the same base and between the same parallels?
In the following figure, PSDA is a parallelogram. Points Q and R are taken on PS such that PQ = QR = RS and PA || QB || RC. Prove that ar (PQE) = ar (CFD).

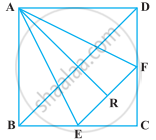
ABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF (Figure), prove that ar (AER) = ar (AFR)
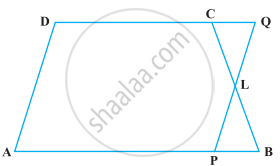
In trapezium ABCD, AB || DC and L is the mid-point of BC. Through L, a line PQ || AD has been drawn which meets AB in P and DC produced in Q (Figure). Prove that ar (ABCD) = ar (APQD)
The diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
