Advertisements
Advertisements
प्रश्न
If from a two-digit number, we subtract the number formed by reversing its digits then the result so obtained is a perfect cube. How many such numbers are possible? Write all of them.
उत्तर
Let ab be any two-digit number.
Then, the digit formed by reversing it digits is ba.
Now, ab – ba = (10a + b) – (10b + a)
= (10a – a) + (b – 10b)
= 9a – 9b
= 9(a – b)
Further, since ab – ba is a perfect cube and is a multiple of 9.
∴ The possible value of a – b is 3.
i.e. a = b + 3
Here, b can take value from 0 to 6.
Hence, possible numbers are as follow.
For b = 0, a = 3, i.e. 30
For b = 1, a = 4, i.e. 41
For b = 2, a = 5, i.e. 52
For b = 3, a = 6, i.e. 63
For b = 4, a = 7, i.e. 74
For b = 5, a = 8, i.e. 85
For b = 6, a = 9, i.e. 96
APPEARS IN
संबंधित प्रश्न
Find the values of the letters in the following and give reasons for the steps involved.
A B
+ 3 7
------
6 A
------
Find the values of the letters in the following and give reasons for the steps involved.
A B
x 5
-------
C A B
-------
If 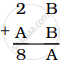 then A = ______ and B = ______.
then A = ______ and B = ______.
If 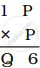 where Q – P = 3, then find the values of P and Q.
where Q – P = 3, then find the values of P and Q.
Find the value of the letters in the following question.
B 6
+ 8 A
C A 2
Find the value of the letters in the following question.
1 B A
+ A B A
8 B 2
Find the value of the letters in the following question.
A A
× A
C A B
212 × 5 is a multiple of 3 and 11. Find the value of x.
A three-digit number 2 a 3 is added to the number 326 to give a three-digit number 5b9 which is divisible by 9. Find the value of b – a.
Find the value of the letters in the following:
P Q
× 6
Q Q Q
