Advertisements
Advertisements
प्रश्न
If the nth term of the A.P. 9, 7, 5, ... is same as the nth term of the A.P. 15, 12, 9, ... find n.
Advertisements
उत्तर
Here, we are given two A.P. sequences whose nth terms are equal. We need to find n.
So let us first find the nth term for both the A.P.
First A.P. is 9, 7, 5 …
Here
First term (a) = 9
Common difference of the A.P. (d) = 7 - 9
= -2
Now as we know
`a_n = a + (n - 1)d`
So for nth term
`a_n = a + (n -1)d`
So for nth term
`a_n = 9 + (n -1)(-2)`
= 9 - 2n + 2
= 11 - 2n .......(1)
Second A.P. is 15, 12, 9 …
Here,
First term (a) = 15
Common difference of the A.P. (d) = 12 - 15
= -3
Now as we know
`a_n = a + (n - 1)d`
So for nth term
`a_n = 15 + (n -1)(-3)`
= 15 - 3n + 3
= 18 - 3n .....(2)
Now, we are given that the nth terms for both the A.P. sequences are equal, we equate (1) and (2),
11 - 2n = 18 - 3n
3n - 2n = 18 - 11
n = 7
Therefore n = 7
APPEARS IN
संबंधित प्रश्न
Find the 9th term from the end (towards the first term) of the A.P. 5, 9, 13, ...., 185
A contract on a construction job specifies a penalty for delay of completion beyond a certain date as follows: Rs. 200 for the first day, Rs. 250 for the second day, Rs. 300 for the third day, etc., the penalty for each succeeding day being Rs. 50 more than for the preceding day. How much money does the contractor have to pay as a penalty if he has delayed the work by 30 days.
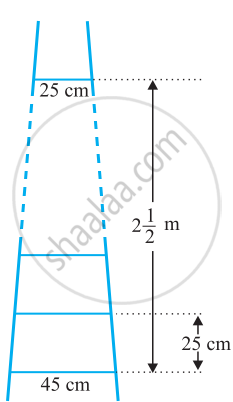
A ladder has rungs 25 cm apart. (See figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are 2 `1/2` m apart, what is the length of the wood required for the rungs?
[Hint: number of rungs = `250/25+ 1`]
Find the sum of first 8 multiples of 3
Find the sum 25 + 28 + 31 + ….. + 100
Find the common difference of an AP whose first term is 5 and the sum of its first four terms is half the sum of the next four terms.
The sum of three consecutive terms of an AP is 21 and the sum of the squares of these terms is 165. Find these terms
In an A.P. the first term is – 5 and the last term is 45. If the sum of all numbers in the A.P. is 120, then how many terms are there? What is the common difference?
The sum of first n terms of an A.P. is 3n2 + 4n. Find the 25th term of this A.P.
The 9th term of an A.P. is 449 and 449th term is 9. The term which is equal to zero is
The common difference of the A.P. is \[\frac{1}{2q}, \frac{1 - 2q}{2q}, \frac{1 - 4q}{2q}, . . .\] is
Q.4
Q.13
How many terms of the A.P. 25, 22, 19, … are needed to give the sum 116 ? Also find the last term.
In an A.P. sum of three consecutive terms is 27 and their products is 504. Find the terms. (Assume that three consecutive terms in an A.P. are a – d, a, a + d.)
Write the formula of the sum of first n terms for an A.P.
If the sum of the first m terms of an AP is n and the sum of its n terms is m, then the sum of its (m + n) terms will be ______.
Complete the following activity to find the 19th term of an A.P. 7, 13, 19, 25, ........ :
Activity:
Given A.P. : 7, 13, 19, 25, ..........
Here first term a = 7; t19 = ?
tn + a + `(square)`d .........(formula)
∴ t19 = 7 + (19 – 1) `square`
∴ t19 = 7 + `square`
∴ t19 = `square`
Find the sum of all odd numbers between 351 and 373.
Three numbers in A.P. have the sum of 30. What is its middle term?
