Advertisements
Advertisements
प्रश्न
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
Proof is lengthy and it is not interesting.
उत्तर
p ∧ ∼ q
APPEARS IN
संबंधित प्रश्न
Examine whether each of the following statement patterns is a tautology or a contradiction or a contingency.
[~(~p ∧ ~q)] v q
Using truth table prove that p ↔ q = (p ∧ q) ∨ (~p ∧ ~q).
Write the following compound statement symbolically.
Nagpur is in Maharashtra and Chennai is in Tamil Nadu.
Write the following compound statement symbolically.
x is not irrational number but is a square of an integer.
Construct the truth table of the following statement pattern.
[(p → q) ∧ q] → p
Express the following statement in symbolic form.
I like playing but not singing.
Write the negation of the following statement.
All men are animals.
Write the negation of the following statement.
It is false that Nagpur is capital of Maharashtra
Write the following statement in symbolic form.
If triangle is equilateral then it is equiangular.
Write the following statement in symbolic form.
If Kutub-Minar is in Delhi then Taj-Mahal is in Agra.
Find the truth value of the following statement.
Every accountant is free to apply his own accounting rules if and only if machinery is an asset.
Find the truth value of the following statement.
3 is a prime number and an odd number.
If p and q are true and r and s are false, find the truth value of the following compound statement.
(p → q) ∨ (r ∧ s)
If p and q are true and r and s are false, find the truth value of the following compound statement.
[(p ∨ s) → r] ∨ ~ [~ (p → q) ∨ s]
Assuming that the following statement is true,
p : Sunday is holiday,
q : Ram does not study on holiday,
find the truth values of the following statements.
Sunday is a holiday and Ram studies on holiday.
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
p ↔ ~ q
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
q ∧ ~ p
Assuming the first statement p and second as q. Write the following statement in symbolic form.
The Sun has set and Moon has risen.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
To be brave is necessary and sufficient condition to climb the Mount Everest.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
x3 + y3 = (x + y)3 if xy = 0.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
It is not true that Ram is tall and handsome.
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
It is interesting iff the proof is lengthy.
Write the negation of the following statement.
I will have tea or coffee.
The negation of the statement (p ˄ q) `→` (r ˅ ∼ p) is ______.
Write the following statements in symbolic form
Milk is white if and only if the sky is not blue
If p : Every natural number is a real number.
q : Every integer is a complex number. Then truth values of p → q and p ↔ q are ______ and ______ respectively.
The symbolic form of the following circuit is (where p, q represents switches S1 and S2 closed respectively)
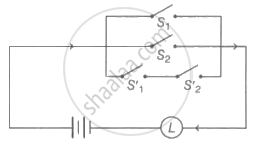
If p and q are true and rands are false statements, then which of the following is true?
Let p : 7 is not greater than 4 and q : Paris is in France by two statements. Then ∼(p ∨ q) is the statement ______
The Boolean expression ∼(q ⇒ ∼p) is equivalent to: ______
The inverse of the statement "If its quality is good. then it is expensive.", is ______
The negation of ∼s ∨ (∼r ∧ s) is equivalent to ______
The statement, 'If I go to school, then I will get knowledge' is equivalent to ______
The negation of the statement: "Getting above 95% marks is a necessary condition for Hema to get admission in good college'' is ______
Which of the following is logically equivalent to `∼(∼p \implies q)`?
The statement ∼(p ↔ ∼q) is ______.
From the following set of statements, select two statements which have similar meaning.
- If a man is judge, then he is honest.
- If a man is not a judge, then he is not honest.
- If a man is honest, then he is a judge.
- If a man is not honest, then he is not a judge.
Construct the truth table for the statement pattern:
[(p → q) ∧ q] → p
